题目内容
6.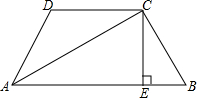 如图,四边形ABCD中,CE⊥AB于E,将①AC平分∠BAD;②CB=CD;③∠B+∠ADC=180°;④AB+AD=2AE中的任意两个作为条件,都可得出另两个结论,请你一一探究,并任选一种情形予以证明.
如图,四边形ABCD中,CE⊥AB于E,将①AC平分∠BAD;②CB=CD;③∠B+∠ADC=180°;④AB+AD=2AE中的任意两个作为条件,都可得出另两个结论,请你一一探究,并任选一种情形予以证明.
分析 取①③作为条件,可得结论②④;在EA上取点EF=BE,连接CF,根据垂直平分线的性质,全等三角形的判定与性质可证CD=CB;根据线段间的和差关系可得AD+AB=2AE.
解答 解:(1)取①③作为条件,可得结论②④;
如图,在EA上取点EF=BE,连接CF,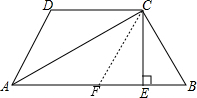
∵CE⊥AB,
∴CF=CB,
∴∠CFB=∠B,
∵∠AFC+∠CFB=180°,∠ADC+∠ABC=180°,
∴∠D=∠AFC,
∵AC平分∠BAD,
即∠DAC=∠FAC,
在△ACD和△ACF中,
$\left\{\begin{array}{l}{∠D=∠AFC}\\{∠DAC=∠FAC}\\{AC=AC}\end{array}\right.$,
∴△ACD≌△ACF(AAS),
∴CD=CF,
∴CD=CB,
∴AD=AF,
∴AD+AB=AF+AE+BE=AF+EF+AE=AE+AE=2AE.
(2)取④③作为条件,可得结论①②;
延长AB到M,使得BM=AD,作AN⊥CD交CD的延长线于N,MG⊥CB交CB的延长线于G.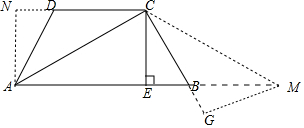
∵AB+AD=2AE,
∴AB+BM=2AE,
∴AE=EM,
∵CE⊥AM,
∴CA=CM,
∴∠CAM=∠M,
∵∠ADC+∠ABC=180°,∠ABC+∠CBM=180°,
∴∠ADC=∠CBM,
∴∠ADN=∠MBG,
∵AD=BM,∠N=∠G=90°,
∴△ADN≌△MBG,
∴AN=GM,DN=BG,
∵AC=CM,
∴Rt△ACN≌△MCG,
∴∠ACN=∠MCG,CN=CG,
∴CD=CB,
∴△DCA≌△BCM,
∴∠DAC=∠CMB,
∴∠CAM=∠CAD,
∴AC平分∠DAE.
点评 本题考查了垂直平分线的性质,全等三角形的判定与性质,关键是作出辅助线构造全等三角形,同时注意线段间的和差关系的运用.

练习册系列答案
相关题目
16.若分式$\frac{x-1}{x+2}$的值为0,则x的值是( )
| A. | -2 | B. | -1 | C. | 1 | D. | 0 |
1.下列图案中既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
16.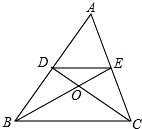 如图已知:△ABC中,DE∥BC,BE,CD交于点O,S△DOE:S△BOC=4:25,则AD:DB=( )
如图已知:△ABC中,DE∥BC,BE,CD交于点O,S△DOE:S△BOC=4:25,则AD:DB=( )
 如图已知:△ABC中,DE∥BC,BE,CD交于点O,S△DOE:S△BOC=4:25,则AD:DB=( )
如图已知:△ABC中,DE∥BC,BE,CD交于点O,S△DOE:S△BOC=4:25,则AD:DB=( )| A. | 2:5 | B. | 2:3 | C. | 4:9 | D. | 3:5 |
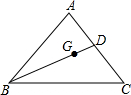 如图,BD是△ABC的中线,G为△ABC的重心,设$\overrightarrow{BA}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,试用$\overrightarrow{a}$,$\overrightarrow{b}$的线性组合表示向量$\overrightarrow{GB}$.
如图,BD是△ABC的中线,G为△ABC的重心,设$\overrightarrow{BA}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,试用$\overrightarrow{a}$,$\overrightarrow{b}$的线性组合表示向量$\overrightarrow{GB}$.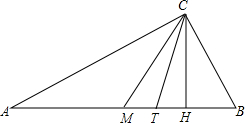 在△ABC中,M是AB中点,CH⊥AB于H,CT是∠ACB和∠MCH的平分线.求证:△ABC是直角三角形.
在△ABC中,M是AB中点,CH⊥AB于H,CT是∠ACB和∠MCH的平分线.求证:△ABC是直角三角形.