题目内容
过点(-1,7)的一条直线与x轴,y轴分别相交于点A,B,且与直线y=-
x+1平行.求在线段AB上,横、纵坐标都是整数的点的坐标.
| 3 |
| 2 |
考点:两条直线相交或平行问题
专题:计算题
分析:设直线AB的解析式为y=kx+b,根据两直线平行的问题得到k=-
,再把(-1,7)代入y=-
x+b得到b=
,则直线AB的解析式为y=-
x+
,接着根据坐标轴上点的坐标特征求出B(0,
),A(
,0),然后分别计算x=1、2、3时的函数值,从而得到在线段AB上,横、纵坐标都是整数的点的坐标.
| 3 |
| 2 |
| 3 |
| 2 |
| 11 |
| 2 |
| 3 |
| 2 |
| 11 |
| 2 |
| 11 |
| 2 |
| 11 |
| 3 |
解答:解:设直线AB的解析式为y=kx+b,
∵直线y=kx+b与直线y=-
x+1平行,
∴k=-
,
把(-1,7)代入y=-
x+b得
+b=7,解得b=
,
∴直线AB的解析式为y=-
x+
,
当x=0时,y=
,则B点坐标为(0,
);当y=0时,-
x+
=0,解得x=
,则A点坐标为(
,0),
当x=1时,y=-
x+
=4;当x=2时,y=-
x+
=
;当x=3时,y=-
x+
=1;
∴在线段AB上,横、纵坐标都是整数的点的坐标为(1,4),(3,1).
∵直线y=kx+b与直线y=-
| 3 |
| 2 |
∴k=-
| 3 |
| 2 |
把(-1,7)代入y=-
| 3 |
| 2 |
| 3 |
| 2 |
| 11 |
| 2 |
∴直线AB的解析式为y=-
| 3 |
| 2 |
| 11 |
| 2 |
当x=0时,y=
| 11 |
| 2 |
| 11 |
| 2 |
| 3 |
| 2 |
| 11 |
| 2 |
| 11 |
| 3 |
| 11 |
| 3 |
当x=1时,y=-
| 3 |
| 2 |
| 11 |
| 2 |
| 3 |
| 2 |
| 11 |
| 2 |
| 5 |
| 2 |
| 3 |
| 2 |
| 11 |
| 2 |
∴在线段AB上,横、纵坐标都是整数的点的坐标为(1,4),(3,1).
点评:本题考查了两直线相交或平行问题:两条直线的交点坐标,就是由这两条直线相对应的一次函数表达式所组成的二元一次方程组的解;若两条直线是平行的关系,那么他们的自变量系数相同,即k值相同.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
下列现象中,可用“两点之间,线段最短”来解释的现象是( )
| A、将弯曲的河道改直,可以缩短航程 |
| B、用两个钉子就可以把木条固定在墙上 |
| C、植树时,只要先定出两棵树的位置,就能确定同一行树所在的直线 |
| D、利用圆规可以比较两条线段的长短关系 |
2014年1月1日零点,北京、上海、重庆、宁夏的气温分别是-4℃,5℃,-6℃,-8℃,这一天中气温最低的是( )
| A、北京 | B、上海市 | C、重庆 | D、宁夏 |
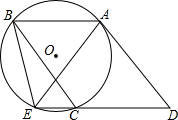 如图,△ABC内接于⊙O,CD∥AB,AD∥BC,DC的延长线交⊙O于E,连接BE、AE.
如图,△ABC内接于⊙O,CD∥AB,AD∥BC,DC的延长线交⊙O于E,连接BE、AE.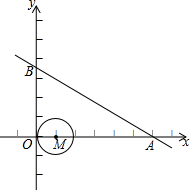 如图,一次函数y=-
如图,一次函数y=-