题目内容
8.先化简,再求值:$\frac{8x}{{x}^{2}+4x+4}$÷$\frac{{x}^{2}-2x}{{x}^{2}-4}$-$\frac{2}{x+2}$,其中x=4cos30°•sin45°-2.分析 根据分式的除法和减法可以化简题目中的式子,然后将x4cos30°•sin45°-2化简求值再代入前面分式化简后的式子即可解答本题.
解答 解:$\frac{8x}{{x}^{2}+4x+4}$÷$\frac{{x}^{2}-2x}{{x}^{2}-4}$-$\frac{2}{x+2}$
=$\frac{8x}{(x+2)^{2}}•\frac{(x+2)(x-2)}{x(x-2)}-\frac{2}{x+2}$
=$\frac{8}{x+2}-\frac{2}{x+2}$
=$\frac{6}{x+2}$,
∵x=4cos30°•sin45°-2=4×$\frac{\sqrt{3}}{2}•\frac{\sqrt{2}}{2}$-2=$\sqrt{6}-2$,
∴当a=$\sqrt{6}-2$时,原式=$\frac{6}{\sqrt{6}-2+2}=\frac{6}{\sqrt{6}}=\sqrt{6}$.
点评 本题考查分式的化简求值、特殊角的三角函数值,解答本题的关键是明确分式化简求值的方法和知道特殊角的三角函数值.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
16.为了检查一批零件的质量,从中抽取10件,测得它们的长度,下列叙述正确的是( )
| A. | 这一批零件的质量全体是总体 | |
| B. | 从中抽取的10件零件是总体的一个样本 | |
| C. | 这一批零件的长度的全体是总体 | |
| D. | 每一个零件的质量为个体 |
13.对于命题“如果∠1+∠2=90°,那么∠1≠∠2”,能说明它是假命题的反例是( )
| A. | ∠1=50°,∠2=40° | B. | ∠1=50°,∠2=50° | C. | ∠1=40°,∠2=40° | D. | ∠1=45°,∠2=45° |
20.-$\sqrt{7}$介于( )
| A. | -4与-3之间 | B. | -3与-2之间 | C. | -2与-1之间 | D. | -1与0之间 |
17.下列各组数中,相等的是( )
| A. | $\frac{{3}^{2}}{4}$与$\frac{9}{16}$ | B. | -(-$\frac{1}{3}$)与|-$\frac{1}{3}$| | C. | (-$\frac{1}{3}$)2与-$\frac{1}{9}$ | D. | $\sqrt{\frac{1}{4}}$与$\root{3}{-\frac{1}{8}}$ |
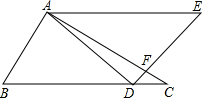 将一副三角板拼成如图所示的图形,即∠BAC=∠ADE=90°,∠DAE=∠E=45°,∠C=30°,∠B=60°,DE与AC相交于点F.
将一副三角板拼成如图所示的图形,即∠BAC=∠ADE=90°,∠DAE=∠E=45°,∠C=30°,∠B=60°,DE与AC相交于点F.