题目内容
19.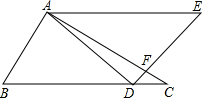 将一副三角板拼成如图所示的图形,即∠BAC=∠ADE=90°,∠DAE=∠E=45°,∠C=30°,∠B=60°,DE与AC相交于点F.
将一副三角板拼成如图所示的图形,即∠BAC=∠ADE=90°,∠DAE=∠E=45°,∠C=30°,∠B=60°,DE与AC相交于点F.(1)如果∠AFD=75°,那么AE与BC平行吗?试说明理由;
(2)如果AE∥BC,写出图中与∠AFD相等的角,说明理由并求出度数.
分析 (1)根据三角形外角性质,可得∠EAF=30°,再根据∠C=30°,可得∠EAF=∠C,进而判定AE∥BC;
(2)首先根据∠BAC与∠B的度数求得∠C的度数,从而得到AE∥BC,利用平行线的性质得到∠CAE=30°,从而求得结论.
解答 解:(1)AE与BC平行.
证明:∵∠AFD是△AEF的外角,
∴∠EAF=∠AFD-∠E=75°-45°=30°,
又∵∠C=30°,
∴∠EAF=∠C,
∴AE∥BC;
(2)∵∠BAC=90°,∠B=60°,
∴∠C=30°,
∵AE∥BC,
∴∠CAE=30°,
∴∠AFD=∠E+∠CAE=75°.
根据对顶角相等,可得∠AFD=∠EFC.
根据三角形内角和定理,可得∠BAD=180°-60°-45°=75°.
故图中与∠AFD相等的角为∠EFC和∠BAD.
点评 本题考查了平行线的判定与性质及三角形的外角的性质,解题时注意:平行线的判定是由角的数量关系判断两直线的位置关系;平行线的性质是由平行关系来寻找角的数量关系.

练习册系列答案
相关题目
7. 如图,是一个几何体的三视图,那么三视图所对应的几何体是( )
如图,是一个几何体的三视图,那么三视图所对应的几何体是( )
 如图,是一个几何体的三视图,那么三视图所对应的几何体是( )
如图,是一个几何体的三视图,那么三视图所对应的几何体是( )| A. |  | B. |  | C. |  | D. |  |
14.下列各式正确的是( )
| A. | -(-2017)=2017 | B. | |-2017|=±2017 | C. | 20170=0 | D. | 2017-1=-2017 |
9.截至5月21日,全县完成工业开票销售337.53亿元,337.53亿元用科学记数法表示为( )元.
| A. | 33.753×109 | B. | 3.3753×1010 | C. | 0.33753×1011 | D. | 0.033753×1012 |

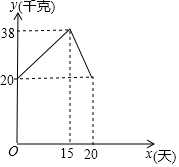 某粮油超市平时每天都将一定数量的某些品种的粮食进行包装以便出售,已知每天包装江米20千克,为迎接今年5月30日的“端午节”,该超市决定在节前20天增加每天包装江米的质量,包装质量与天数的变化情况如图所示,节日后又恢复到原来每天包装的质量.
某粮油超市平时每天都将一定数量的某些品种的粮食进行包装以便出售,已知每天包装江米20千克,为迎接今年5月30日的“端午节”,该超市决定在节前20天增加每天包装江米的质量,包装质量与天数的变化情况如图所示,节日后又恢复到原来每天包装的质量.