题目内容
9.已知点M为抛物线y=x2+bx+b的顶点,抛物线与x轴无交点,点N在抛物线的对称轴上且位于点M上方.若点N到点M的距离是点M到x轴距离的两倍,直线ON的解析式为y=kx,请求出k关于b的函数关系式.分析 利用配方法求出点M坐标,根据条件求出点N坐标代入y=kx,求出k,再根据△<0确定b的取值范围即可.
解答 解:y=x2+bx+b=(x+$\frac{b}{2}$)2+$\frac{4b-{b}^{2}}{4}$,
∴点M坐标(-$\frac{b}{2}$,$\frac{4b-{b}^{2}}{4}$),抛物线对称轴x=-$\frac{b}{2}$,
∴点N的横坐标为-$\frac{b}{2}$,
点N的纵坐标为$\frac{4b-{b}^{2}}{4}$+$\frac{8b-2{b}^{2}}{4}$=$\frac{12b-3{b}^{2}}{4}$,
∴N(-$\frac{b}{2}$,$\frac{12b-3{b}^{2}}{4}$),代入y=kx得到
k×(-$\frac{b}{2}$)=$\frac{12b-3{b}^{2}}{4}$,
∴k=$\frac{3}{2}$b-6,
∵抛物线与x轴无交点,
∴△=b2-4b<0,
∴0<b<4,
∴k=$\frac{3}{2}$b-6 (0<b<4).
点评 本题考查抛物线与x轴解得问题、配方法求顶点坐标等知识,解题的关键是知道抛物线与x轴交点情况可以用△的值判定,灵活掌握待定系数法,属于中考常考题型.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
17.已知等腰三角形的底边长为10,腰长为13,则一腰上的高为( )
| A. | 12 | B. | $\frac{60}{13}$ | C. | $\frac{120}{13}$ | D. | $\frac{13}{5}$ |
1.下列运算正确的是( )
| A. | -30=1 | B. | 3-2=-6 | C. | $\sqrt{9}=±3$ | D. | -32=-9 |
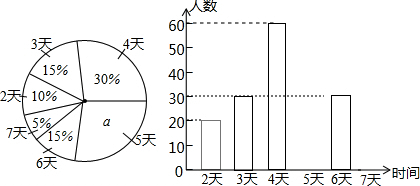
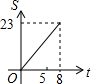
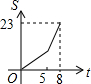
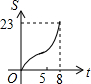
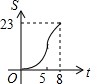
 如图,向放有一个圆柱体的长方体水槽注水(速度一定),直至注满水槽,则下列图象中能反应水槽中水面上升高度h与注水时间t之间函数关系的是( )
如图,向放有一个圆柱体的长方体水槽注水(速度一定),直至注满水槽,则下列图象中能反应水槽中水面上升高度h与注水时间t之间函数关系的是( )



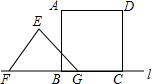 如图,正方形ABCD边长为8cm,FG是等腰直角△EFG的斜边,FG=10cm,点B、F、C、G都在直线l上,△EFG以1cm/s的速度沿直线l向右做匀速运动,当t=0时,点G与B重合,记t(0≤t≤8)秒时,正方形与三角形重合部分的面积是Scm2,则S与t之间的函数关系图象大致为( )
如图,正方形ABCD边长为8cm,FG是等腰直角△EFG的斜边,FG=10cm,点B、F、C、G都在直线l上,△EFG以1cm/s的速度沿直线l向右做匀速运动,当t=0时,点G与B重合,记t(0≤t≤8)秒时,正方形与三角形重合部分的面积是Scm2,则S与t之间的函数关系图象大致为( )