题目内容
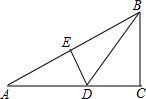 已知:如图所示,△ABC中,∠C=90°,DE是AB边的中垂线,E为垂足,DE交AC边于点D.若设∠A=x°,∠BDC=y°,
已知:如图所示,△ABC中,∠C=90°,DE是AB边的中垂线,E为垂足,DE交AC边于点D.若设∠A=x°,∠BDC=y°,①变量y是否可以看作变量x的函数?若变量y是变量x的函数,写出y关于x的函数解析式,并写出函数定义域;若变量y不是变量x的函数,请说明理由.
②求当x等于多少时,BD平分∠ABC.
考点:线段垂直平分线的性质,函数关系式,角平分线的性质
专题:
分析:①根据线段垂直平分线的性质得出∠A=∠ABD,再由三角形外角的性质即可得出结论;
②根据角平分线的性质及直角三角形的性质即可得出结论.
②根据角平分线的性质及直角三角形的性质即可得出结论.
解答:解:①∵DE是AB边的中垂线,∠A=x°,
∴∠A=∠ABD=x°,
∵∠BDC是△ABD的外角,
∴∠BDC=∠A+∠ABD=2∠A,
∵∠BDC=y°,
∴y=2x(0<x<90);
②∵由(1)知,∠A=∠ABD=x°,
∴∠A=∠ABD=∠DBC=x°,
∵∠C=90°,
∴∠A+∠ABD+∠DBC=90°,即3x°=90°,解得x=30.
∴∠A=∠ABD=x°,
∵∠BDC是△ABD的外角,
∴∠BDC=∠A+∠ABD=2∠A,
∵∠BDC=y°,
∴y=2x(0<x<90);
②∵由(1)知,∠A=∠ABD=x°,
∴∠A=∠ABD=∠DBC=x°,
∵∠C=90°,
∴∠A+∠ABD+∠DBC=90°,即3x°=90°,解得x=30.
点评:本题考查的是线段垂直平分线的性质,熟知线段垂直平分线上任意一点,到线段两端点的距离相等是解答此题的关键.

练习册系列答案
相关题目
雅安地震后,某小组6名同学积极参加班级组织的为灾区捐款活动,他们捐款的数额分别是(单位:元):50,30,50,50,40,70.这组数据的中位数和众数分别是( )
| A、40,50 |
| B、45,50 |
| C、50,50 |
| D、50,70 |
 如图,将一张等腰梯形纸片沿中位线剪开,拼成一个新的图形,这个新的图形可以是下列图形中的( )
如图,将一张等腰梯形纸片沿中位线剪开,拼成一个新的图形,这个新的图形可以是下列图形中的( )| A、三角形 | B、平行四边形 |
| C、矩形 | D、正方形 |

 解不等式组
解不等式组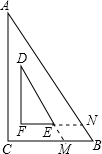 如图,是一块学生用的直角三角板ABC,其中∠A=30°,斜边AB=8cm,里面空心△DEF的各边与△ABC的对应边平行,且各对应边间的距离都是1cm,延长DE交BC于点M,延长FE交AB于点N.
如图,是一块学生用的直角三角板ABC,其中∠A=30°,斜边AB=8cm,里面空心△DEF的各边与△ABC的对应边平行,且各对应边间的距离都是1cm,延长DE交BC于点M,延长FE交AB于点N.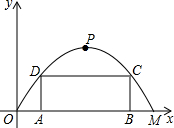 如图,龙丽公路某隧道横截面为抛物线,其最大高度为9米,底部宽度OM为18米. 现以O点为原点,OM所在直线为x轴建立直角坐标系.
如图,龙丽公路某隧道横截面为抛物线,其最大高度为9米,底部宽度OM为18米. 现以O点为原点,OM所在直线为x轴建立直角坐标系.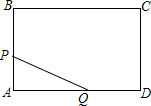 如图,在长方形ABCD中,AB=6cm,BC=8cm,某个时刻点P从A出发,沿着A→B→C在边上运动,速度为1cm/s,与此同时,点Q从D出发,速度为2cm/s,沿着D→A→B→C的方向追点P.
如图,在长方形ABCD中,AB=6cm,BC=8cm,某个时刻点P从A出发,沿着A→B→C在边上运动,速度为1cm/s,与此同时,点Q从D出发,速度为2cm/s,沿着D→A→B→C的方向追点P.