题目内容
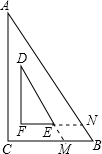 如图,是一块学生用的直角三角板ABC,其中∠A=30°,斜边AB=8cm,里面空心△DEF的各边与△ABC的对应边平行,且各对应边间的距离都是1cm,延长DE交BC于点M,延长FE交AB于点N.
如图,是一块学生用的直角三角板ABC,其中∠A=30°,斜边AB=8cm,里面空心△DEF的各边与△ABC的对应边平行,且各对应边间的距离都是1cm,延长DE交BC于点M,延长FE交AB于点N.(1)判断四边形EMBN的形状,并说明理由;
(2)求△DEF的周长.
考点:相似三角形的应用,位似变换
专题:
分析:(1)根据空心△DEF的各边与△ABC的对应边平行直接得到两组对边平行,用平行四边形的定义判定平行四边形即可;
(2)连接BE,作EH⊥BC,FM⊥BC,即可求得EF的长,则在直角△DEF中,即可解得DE,DF的长,从而求得三角形的周长.
(2)连接BE,作EH⊥BC,FM⊥BC,即可求得EF的长,则在直角△DEF中,即可解得DE,DF的长,从而求得三角形的周长.
解答: 解:(1)∵空心△DEF的各边与△ABC的对应边平行,
解:(1)∵空心△DEF的各边与△ABC的对应边平行,
∴EM∥BN,EN∥MB,
∴四边形EMBN是平行四边形;
(2)连接BE,作EH⊥BC,FG⊥BC,则CG=1cm.
∵直角△ABC中,∠A=30°,
∴BC=
AB=
×8=4.
∵E到AB与到BC的距离相等,
∴BE平分∠ABC.
∴∠EBN=30°
在直角△BHE中,tan∠EBH=
.
∴BH=
=
EH=
.
∴EF=NG=4-BH-CG=4-
-1=3-
.
在直角△DEF中,∠D=30°,
∴DE=2EF=6-2
,
DF=
EF=3
-3.
∴△DEF的周长是EF+DE+DF=3-
+6-2
+3
-3=6.
 解:(1)∵空心△DEF的各边与△ABC的对应边平行,
解:(1)∵空心△DEF的各边与△ABC的对应边平行,∴EM∥BN,EN∥MB,
∴四边形EMBN是平行四边形;
(2)连接BE,作EH⊥BC,FG⊥BC,则CG=1cm.
∵直角△ABC中,∠A=30°,
∴BC=
| 1 |
| 2 |
| 1 |
| 2 |
∵E到AB与到BC的距离相等,
∴BE平分∠ABC.
∴∠EBN=30°
在直角△BHE中,tan∠EBH=
| EH |
| BH |
∴BH=
| EH |
| tan30° |
| 3 |
| 3 |
∴EF=NG=4-BH-CG=4-
| 3 |
| 3 |
在直角△DEF中,∠D=30°,
∴DE=2EF=6-2
| 3 |
DF=
| 3 |
| 3 |
∴△DEF的周长是EF+DE+DF=3-
| 3 |
| 3 |
| 3 |
点评:本题考查了相似三角形的应用及含30°锐角的直角三角形的性质,关键是作出辅助线求得EF的长.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案
相关题目
若长方形的周长为16,其邻边a、b为整数,且满足a2+b2+3ab=76,则长方形的面积为( )
| A、6 | B、8 | C、10 | D、12 |
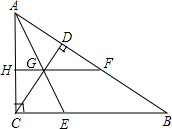 如图,在△ABC中,∠ACB=90°,CD⊥AB于D. 把三角形沿AE对折使点C落在AB边上的点F上,CD与折痕AE相交于G,连结FG并延长交AC于H.
如图,在△ABC中,∠ACB=90°,CD⊥AB于D. 把三角形沿AE对折使点C落在AB边上的点F上,CD与折痕AE相交于G,连结FG并延长交AC于H.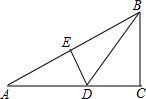 已知:如图所示,△ABC中,∠C=90°,DE是AB边的中垂线,E为垂足,DE交AC边于点D.若设∠A=x°,∠BDC=y°,
已知:如图所示,△ABC中,∠C=90°,DE是AB边的中垂线,E为垂足,DE交AC边于点D.若设∠A=x°,∠BDC=y°, 探究:如图,长方形ABCD的长为4,宽为2.
探究:如图,长方形ABCD的长为4,宽为2. 如图,△ABC中,AB=AC,AD⊥BC于D,将△ADC绕点A顺时针旋转,至△AEB位置(AC,AB重合),延长AE、CB交于M,延长EB,AD交于N.求证:
如图,△ABC中,AB=AC,AD⊥BC于D,将△ADC绕点A顺时针旋转,至△AEB位置(AC,AB重合),延长AE、CB交于M,延长EB,AD交于N.求证: