题目内容
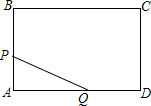 如图,在长方形ABCD中,AB=6cm,BC=8cm,某个时刻点P从A出发,沿着A→B→C在边上运动,速度为1cm/s,与此同时,点Q从D出发,速度为2cm/s,沿着D→A→B→C的方向追点P.
如图,在长方形ABCD中,AB=6cm,BC=8cm,某个时刻点P从A出发,沿着A→B→C在边上运动,速度为1cm/s,与此同时,点Q从D出发,速度为2cm/s,沿着D→A→B→C的方向追点P.(1)点Q能否追上点P?若能,请求出在哪个位置追上;若不能,请说明理由.
(2)当点P还在A→B段运动时,某个时刻△APQ的面积正好是长方形ABCD面积的
| 1 |
| 16 |
考点:一元二次方程的应用
专题:几何动点问题
分析:(1)根据已知求出AD的长,再根据若点Q能追上点P,得出2t-t=8,求出t的值即可得出答案;
(2)根据三角形的面积公式表示出△APQ的面积,再根据△APQ的面积正好是长方形ABCD面积的
,列出方程,再进行求解即可.
(2)根据三角形的面积公式表示出△APQ的面积,再根据△APQ的面积正好是长方形ABCD面积的
| 1 |
| 16 |
解答:解:(1)能追上,理由如下:
∵BC=8cm,
∴AD=8cm,
∴若点Q能追上点P,则2t-t=8,
∴t=8,
∴点P在BC上,且离B点2厘米出能追上;
(2)当△APQ的面积正好是长方形ABCD面积的
时,根据题意得:
×(8-2t)•t=
×6×8,
解得:t=1或t=3.
答:此时对应的时刻t的值是1或3.
∵BC=8cm,
∴AD=8cm,
∴若点Q能追上点P,则2t-t=8,
∴t=8,
∴点P在BC上,且离B点2厘米出能追上;
(2)当△APQ的面积正好是长方形ABCD面积的
| 1 |
| 16 |
| 1 |
| 2 |
| 1 |
| 16 |
解得:t=1或t=3.
答:此时对应的时刻t的值是1或3.
点评:此题考查了一元二次方程的应用,关键是根据题意找出题目中的等量关系,列出方程,用到的知识点是三角形的面积公式、解一元二次方程.

练习册系列答案
相关题目
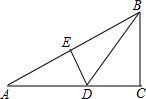 已知:如图所示,△ABC中,∠C=90°,DE是AB边的中垂线,E为垂足,DE交AC边于点D.若设∠A=x°,∠BDC=y°,
已知:如图所示,△ABC中,∠C=90°,DE是AB边的中垂线,E为垂足,DE交AC边于点D.若设∠A=x°,∠BDC=y°,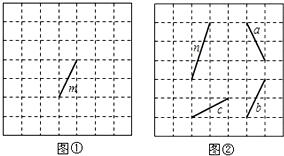 (1)在图①中.以线段m为一边画菱形,要求菱形的顶点均在格点上.
(1)在图①中.以线段m为一边画菱形,要求菱形的顶点均在格点上.