题目内容
9.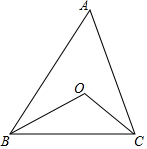 如图:BO、CO分别平分∠ABC和∠ACB,
如图:BO、CO分别平分∠ABC和∠ACB,(1)若∠A=40°,求∠O的度数;
(2)若∠A=60°或∠A=100°时,∠O等于多少度?
(3)由(1)、(2)你发现了什么规律?
(4)利用你得出的结论,求当∠O=150°时,∠A的度数(直接写出答案).
(提示:三角形的内角和等于180°)
分析 根据三角形内角和定理、角平分线的定义解答即可.
解答 解:(1)∵∠A=40°,
∴∠ABC+∠ACB=180°-∠A=140°,
∵BO、CO分别平分∠ABC和∠ACB,
∴∠OBC+∠OCB=$\frac{1}{2}$(∠ABC+∠ACB)=70°,
∴∠O=180°-70°=110°;
(2)由(1)得,
当∠A=60°时,∠OBC+∠OCB=$\frac{1}{2}$(∠ABC+∠ACB)=60°,
∴∠O=180°-60°=120°,
当∠A=100°时,∠OBC+∠OCB=$\frac{1}{2}$(∠ABC+∠ACB)=40°,
∴∠O=180°-40°=140°;
(3)由(1)、(2)得,∠O=90°+$\frac{1}{2}$∠A;
(4)当∠O=150°时,∠A=2∠O-180°=120°.
点评 本题考查的是三角形的内角和定理,掌握三角形内角和等于180°是解题的关键.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
19.若∠α与∠β互余,且∠α:∠β=3:2,那么∠α与∠β的度数分别是( )
| A. | 36°,54° | B. | 60°,40° | C. | 54°,36° | D. | 72°,108° |
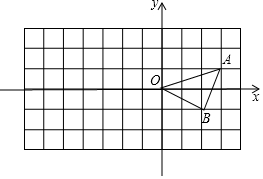 方格纸中每个小正方形的边长都是单位1,△OAB在平面直角坐标系中的位置如图所示.解答问题:
方格纸中每个小正方形的边长都是单位1,△OAB在平面直角坐标系中的位置如图所示.解答问题: