题目内容
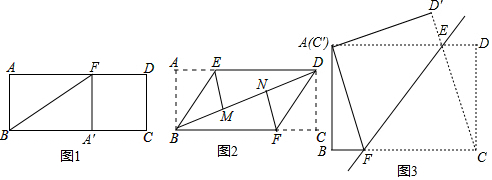
1. 已知:如图,平行四边形ABCD的对角线相交于点O,点E在边BC的延长线上,且OE=OB,联结DE.
已知:如图,平行四边形ABCD的对角线相交于点O,点E在边BC的延长线上,且OE=OB,联结DE.(1)求证:DE⊥BE;
(2)设CD与OE交于点F,若OF2+FD2=OE2,CE=3,DE=4,求线段CF的长.
分析 (1)先根据平行四边形的性质,得出OD=OB,再根据OE=OB,得出OE=OB=OD,最后根据三角形内角和定理,求得∠OEB+∠OED=90°,即可得出结论.
(2)证明△OFD为直角三角形,得出∠OFD=90°.在Rt△CED中,由勾股定理求出CD=5.由三角形面积求出$EF=\frac{12}{5}$.在Rt△CEF中,根据勾股定理求出CF即可.
解答 (1)证明:∵平行四边形ABCD,
∴OB=OD.
∵OB=OE,
∴OE=OD.
∴∠OED=∠ODE.
∵OB=OE,
∴∠OBE=∠OEB.
∵∠OBE+∠OEB+∠ODE+∠OED=180°,
∴∠OEB+∠OED=90°.
∴DE⊥BE;
(2)解:∵OE=OD,OF2+FD2=OE2,
∴OF2+FD2=OD2.
∴△OFD为直角三角形,且∠OFD=90°.
在Rt△CED中,∠CED=90°,CE=3,DE=4,
∴CD2=CE2+DE2.
∴CD=5.
又∵$\frac{1}{2}CD•EF=\frac{1}{2}CE•DE$,
∴$EF=\frac{12}{5}$.
在Rt△CEF中,∠CFE=90°,CE=3,$EF=\frac{12}{5}$,
根据勾股定理得:$CF=\frac{9}{5}$.
点评 本题主要考查了平行四边形的性质、等腰三角形的性质、勾股定理和勾股定理的逆定理,熟练掌握平行四边形的性质以及勾股定理的逆定理是关键.

练习册系列答案
相关题目
11.计算正确的是( )
| A. | 3.4×104=340000 | B. | m×2m2=3m2 | C. | (-$\frac{1}{2}$mn2)2=m2n4 | D. | 4xy-4yx=0 |
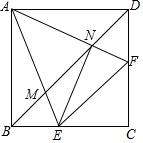 如图,在正方形ABCD 中,点E,F分别在边BC,DC上,AE、AF分别交BD于点M,N,连接CN、EN,且CN=EN.下列结论:①AN=EN,AN⊥EN;②BE+DF=EF;③∠DFE=2∠AMN;④EF2=2BM2+2DN2;⑤图中只有4对相似三角形.其中正确结论的个数是( )
如图,在正方形ABCD 中,点E,F分别在边BC,DC上,AE、AF分别交BD于点M,N,连接CN、EN,且CN=EN.下列结论:①AN=EN,AN⊥EN;②BE+DF=EF;③∠DFE=2∠AMN;④EF2=2BM2+2DN2;⑤图中只有4对相似三角形.其中正确结论的个数是( ) 尺规作图:请在原图上作一个∠AOC,使∠AOC=2∠AOB,不写已知、求作和作法,保留作图痕迹,在所作图中标上必要的字母.
尺规作图:请在原图上作一个∠AOC,使∠AOC=2∠AOB,不写已知、求作和作法,保留作图痕迹,在所作图中标上必要的字母.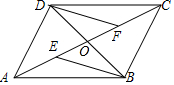 如图,四边形ABCD的对角线AC、BD相交于点O,且O是AC的中点,AE=CF,DF∥BE.
如图,四边形ABCD的对角线AC、BD相交于点O,且O是AC的中点,AE=CF,DF∥BE. 如图,?ABCD中,G是CD的中点,E是边长AD上的动点,EG的延长线与BC的延长线相交于点F,连接CE,DF.
如图,?ABCD中,G是CD的中点,E是边长AD上的动点,EG的延长线与BC的延长线相交于点F,连接CE,DF.