题目内容
6.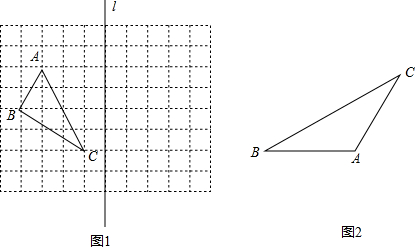 (1)如图1,在边长为1的小正方形组成的网格中,△ABC的三个顶点分别在格点上,请在网格中按要求作出下列图形,并标注相应的字母.
(1)如图1,在边长为1的小正方形组成的网格中,△ABC的三个顶点分别在格点上,请在网格中按要求作出下列图形,并标注相应的字母.①作△A1B1C1,使得△A1B1C1与△ABC关于直线l对称;
②△A1B1C1得面积为4.
(2)已知:如图2,△ABC
①用直尺和圆规分别作AB、AC的垂直平分线,其交点为M (保留作图痕迹,不写作法).
②猜想CM、BM、AM之间的数量关系为AM=BM=CM.
分析 (1)①首先确定A、B、C三点关于l的对称点A1、B1、C1,再连接即可;
②利用矩形的面积减去周围多余三角形的面积即可;
(2)①分别以B、A为圆心,大于$\frac{1}{2}$AB长为半径画弧,两弧有两个交点,再过两交点画直线,同法作AC的垂直平分线,两垂直平分线的交点记作M;
②连接BM、AM、CM,根据线段垂直平分线的性质可得MA=MB,MA=MC,进而可得答案.
解答  解:(1)①如图1所示:
解:(1)①如图1所示:
②△A1B1C1得面积:3×4-$\frac{1}{2}$×2×4-$\frac{1}{2}$×2×1-$\frac{1}{2}$×2×3=4,
故答案为:4;
(2)①如图2所示:
②连接BM、AM、CM,
∵MN是AB的垂直平分线,
∴MA=MB,
∵ME是AC的垂直平分线,
∴MA=MC,
∴AM=BM=CM,
故答案为:AM=BM=CM.
点评 此题主要考查了作图--轴对称变换,以及基本作图,关键是掌握线段垂直平分线的做法和性质.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
16.将抛物线y1=-x2平移后得到y2=-x2+2x-2,则把抛物线y1平移到y2的方法是( )
| A. | 先向左平移1个单位,再向下平移1个单位 | |
| B. | 先向左平移1个单位,再向上平移1个单位 | |
| C. | 先向右平移1个单位,再向下平移1个单位 | |
| D. | 先向有平移1个单位,再向上平移1个单位 |
11.如图1,在矩形ABCD中,动点P从点B出发,沿BC、CD、DA运动至点A停止,设点P运动的路程为x,△ABP的面积为y,如果y关于x的函数图象如图2所示,则△ABC的面积是( )


| A. | 10 | B. | 16 | C. | 18 | D. | 20 |
18. 如图是由5个相同的小正方体构成的几何体,其左视图是( )
如图是由5个相同的小正方体构成的几何体,其左视图是( )
 如图是由5个相同的小正方体构成的几何体,其左视图是( )
如图是由5个相同的小正方体构成的几何体,其左视图是( )| A. |  | B. |  | C. |  | D. |  |
 如图,将一张长方形纸片ABCD沿EF折叠后,点D,C分别落在D′,C′地位置,ED′的延长线与BC相交于点G,若∠EFG=68°,则∠1的度数是136°.
如图,将一张长方形纸片ABCD沿EF折叠后,点D,C分别落在D′,C′地位置,ED′的延长线与BC相交于点G,若∠EFG=68°,则∠1的度数是136°. 如图,已知反比例函数y=$\frac{6}{x}$的图象与正比例函数y=$\frac{2}{3}$x的图象交于A、B两点,B点坐标为(-3,-2),则A点的坐标为(3,2)
如图,已知反比例函数y=$\frac{6}{x}$的图象与正比例函数y=$\frac{2}{3}$x的图象交于A、B两点,B点坐标为(-3,-2),则A点的坐标为(3,2)


