题目内容
14．
如图，将一张长方形纸片ABCD沿EF折叠后，点D，C分别落在D′，C′地位置，ED′的延长线与BC相交于点G，若∠EFG=68°，则∠1的度数是136°．
分析 由AD∥BC，∠EFG=68°，根据两直线平行，内错角相等，可求得∠DEF的度数，然后由折叠的性质，求得∠DEG的度数，继而求得答案．
解答 解：∵AD∥BC，∠EFG=68°，
∴∠DEF=∠EFG=68°，
由折叠的性质可得：∠FEG=∠DEF=68°，
∴∠DEG=∠DEF+∠FEG=136°，
∵AD∥BC，
∴∠1=∠DEG=136°．
故答案为：136°．
点评 此题考查了平行线的性质以及折叠的性质．注意掌握折叠前后图形的对应关系是解此题的关键．
练习册系列答案
同步练习强化拓展系列答案
相关题目
△ABC中，AB=5，AC=4，BC=6．
5．a、b都是实数，且a＜b，则下列不等式的变形正确的是（ ）
| A． | ac＜bc | B． | a+x＞b+x | C． | -a＞-b | D． | $\frac{a}{c}＜\frac{b}{c}$ |
19．
二次函数y=a（x+m）2+n的图象如图，则一次函数y=mx+n的图象经过（ ）
二次函数y=a（x+m）2+n的图象如图，则一次函数y=mx+n的图象经过（ ）| A． | 二、三、四象限 | B． | 一、二、四象限 | C． | 一、三、四象限 | D． | 一、二、三象限 |
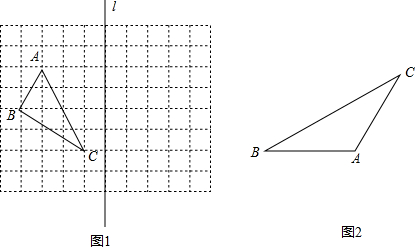（1）如图1，在边长为1的小正方形组成的网格中，△ABC的三个顶点分别在格点上，请在网格中按要求作出下列图形，并标注相应的字母．