题目内容
17．已知数轴上点A、B所对应的实数分别是-$\sqrt{3}$和1，则AB=1+$\sqrt{3}$．分析 根据题意可知A点在原点左边，离原点距离为$\sqrt{3}$，B点在原点右边，离原点距离为1，由此列出算式求AB．
解答 解：依题意，得AB=1-（-$\sqrt{3}$）=1+$\sqrt{3}$．
故答案为：1+$\sqrt{3}$．
点评 本题考查了实数与数轴的关系．关键是明确数对应的点与原点的距离．
练习册系列答案
小博士期末闯关100分系列答案
名校名师培优作业本加核心试卷系列答案
相关题目
7．一次函数y=x+1的图象是（ ）
| A． | 线段 | B． | 抛物线 | C． | 直线 | D． | 双曲线 |
8．为了贯彻落实市委政府提出的“精准扶贫”精神，某校特制定了一系列帮扶A、B两贫困村的计划，现决定从某地运送152箱鱼苗到A、B两村养殖，若用大小货车共15辆，则恰好能一次性运完这批鱼苗，已知这两种大小货车的载货能力分别为12箱/辆和8箱/辆，其运往A、B两村的运费如表：
（1）求这15辆车中大小货车各多少辆？
（2）现安排其中10辆货车前往A村，其余货车前往B村，设前往A村的大货车为x辆，前往A、B两村总费用为y元，试求出y与x的函数解析式．
（3）在（2）的条件下，若运往A村的鱼苗不少于100箱，请你写出使总费用最少的货车调配方案，并求出最少费用．
| 车型 | 目的地 | |
| A村（元/辆） | B村（元/辆） | |
| 大货车 | ||
| 800 | 900 | |
| 小货车 | 400 | 600 |
（2）现安排其中10辆货车前往A村，其余货车前往B村，设前往A村的大货车为x辆，前往A、B两村总费用为y元，试求出y与x的函数解析式．
（3）在（2）的条件下，若运往A村的鱼苗不少于100箱，请你写出使总费用最少的货车调配方案，并求出最少费用．
5．a、b都是实数，且a＜b，则下列不等式的变形正确的是（ ）
| A． | ac＜bc | B． | a+x＞b+x | C． | -a＞-b | D． | $\frac{a}{c}＜\frac{b}{c}$ |
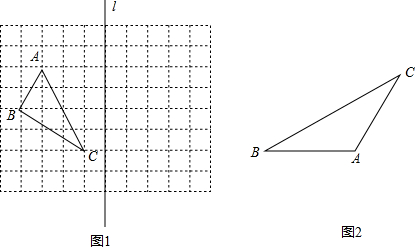（1）如图1，在边长为1的小正方形组成的网格中，△ABC的三个顶点分别在格点上，请在网格中按要求作出下列图形，并标注相应的字母．