题目内容
 如图,一货轮在B处测得灯塔A在货轮的北偏西30°的方向上,随后货轮以30海里/时的速度沿北偏东45°方向航行,40分钟到达C处,此时又测得灯塔A在货轮的北偏西75°的方向上.
如图,一货轮在B处测得灯塔A在货轮的北偏西30°的方向上,随后货轮以30海里/时的速度沿北偏东45°方向航行,40分钟到达C处,此时又测得灯塔A在货轮的北偏西75°的方向上.(1)求此时货轮距灯塔A的距离AC(结果保留根号);
(2)当货轮航行至点C处时,一快艇从B处出发沿货轮的航线追赶货轮,货轮继续按原来方向和速度航行,恰好在灯塔A的正东方向的D点处追上货轮,则快艇的速度为每小时多少海里?
考点:解直角三角形的应用-方向角问题
专题:
分析:(1)根据题意首先求出BC的长,进而得出BH,AH的长,即可得出答案;
(2)首先求出BE的长,进而得出BD的长,即可得出快艇的速度.
(2)首先求出BE的长,进而得出BD的长,即可得出快艇的速度.
解答: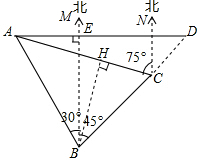 解:(1)如图所示:过点B作BH⊥AC于点H,由题意可得:
解:(1)如图所示:过点B作BH⊥AC于点H,由题意可得:
BC=30×
=20(海里),∠ABM=30°,∠DBM=45°,∠ACN=75°,
则∠ABC=∠ACM+∠CBM=75°,
∵BM∥CN,
∴∠BCN=180°-∠CBM=135°,
∴∠ACB=∠BCN-∠ACB=60°,
∴∠BAC=180°-∠ABC-∠ACB=45°,
在Rt△BCH和Rt△ABH中,
∠CBH=30°,∠ABH=45°,
则CH=
BC=10,BH=
=10
,AH=BH=10
,
故AC=AH+CH=10+10
,
此时货轮距灯塔A的距离AC为:(10+10
)海里;
(2)在Rt△ABH中,AB=
=10
,
设BM与AD交于点E,由题意可得:BM⊥AD,
在Rt△ABE中,∠AEB=90°,∠ABE=30°,
故AE=
AB=5
,BE=
=15
,
在Rt△BDE中,∠BED=90°,∠DBE=45°,
故BD=
=
=30(海里),
故CD=BD-BC=10(海里),
30÷(10÷30)=90(海里/小时),
即快艇的速度为每小时90海里.
 解:(1)如图所示:过点B作BH⊥AC于点H,由题意可得:
解:(1)如图所示:过点B作BH⊥AC于点H,由题意可得:BC=30×
| 40 |
| 60 |
则∠ABC=∠ACM+∠CBM=75°,
∵BM∥CN,
∴∠BCN=180°-∠CBM=135°,
∴∠ACB=∠BCN-∠ACB=60°,
∴∠BAC=180°-∠ABC-∠ACB=45°,
在Rt△BCH和Rt△ABH中,
∠CBH=30°,∠ABH=45°,
则CH=
| 1 |
| 2 |
| BC2-CH2 |
| 3 |
| 3 |
故AC=AH+CH=10+10
| 3 |
此时货轮距灯塔A的距离AC为:(10+10
| 3 |
(2)在Rt△ABH中,AB=
| AH2+BH2 |
| 6 |
设BM与AD交于点E,由题意可得:BM⊥AD,
在Rt△ABE中,∠AEB=90°,∠ABE=30°,
故AE=
| 1 |
| 2 |
| 6 |
| AB2-AE2 |
| 2 |
在Rt△BDE中,∠BED=90°,∠DBE=45°,
故BD=
| BE |
| cos∠DBE |
15
| ||
| cos45° |
故CD=BD-BC=10(海里),
30÷(10÷30)=90(海里/小时),
即快艇的速度为每小时90海里.
点评:此题主要考查了解直角三角形的应用,根据题意正确构造直角三角形是解题关键.

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
 有理数a在数轴上位置如图,则下列结论中正确的是( )
有理数a在数轴上位置如图,则下列结论中正确的是( )| A、a+3是正数 |
| B、a+3是负数 |
| C、a-3是正数 |
| D、a-3为0 |
 在△ABC中,∠A=30°,FB=AF=FD=2,则BD=( )
在△ABC中,∠A=30°,FB=AF=FD=2,则BD=( )| A、1 | B、2 | C、3 | D、4 |
 已知圆锥的全面积为28π,侧面展图的圆心角为60°,求圆锥的侧面积.
已知圆锥的全面积为28π,侧面展图的圆心角为60°,求圆锥的侧面积.