��Ŀ����
3��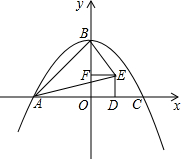 ��ͼ�����κ���y=-$\frac{1}{k}$x2+k��k��0����ͼ����x���ཻ��A��C���㣨��A�ڵ�C����ࣩ����y�ύ�ڵ�B����DΪ�߶�OC��һ�㣨�����O��C�غϣ�����ODΪ��������������ODEF������AE��BE��AB��AB�����D�ĺ�����Ϊm��
��ͼ�����κ���y=-$\frac{1}{k}$x2+k��k��0����ͼ����x���ཻ��A��C���㣨��A�ڵ�C����ࣩ����y�ύ�ڵ�B����DΪ�߶�OC��һ�㣨�����O��C�غϣ�����ODΪ��������������ODEF������AE��BE��AB��AB�����D�ĺ�����Ϊm����1����k=3��m=2ʱ��S��ABE=$\frac{9}{2}$��
��k=4��m=3ʱ��S��ABE=8��
��k=5��m=4ʱ��S��ABE=$\frac{25}{2}$��
��2�����ݣ�1���еĽ��������S��ABE�Ĵ�С����֤����IJ��룻
��3����S��ABE=8ʱ��������ƽ������һ��P���������Ϊn������A��B��E��PΪ������ı���Ϊƽ���ı���ʱ����ֱ��д��m��n����Ĺ�ϵʽ��
���� ��1����y=0�������x��һԪ���η��̵ó�x��ֵ�����ɵ�֪��A�����꣬��x=0���yֵ���ɴ˵ó�B������꣬�ٸ����������ε������Լ�D��ĺ�����Ϊm�ó���D����E�����꣬����k��m��ֵ�ó���A��B��E��D�ĵ�����꣬�ٸ��������ε������ʽ���ɵó����ۣ�
��2��S��ABE=$\frac{1}{2}{k}^{2}$���ɣ�1���ó���k��m��ʾ�ĵ�A��B��E��D�ĵ�����꣬��������ε������ʽ���S��ABE���ɵó����ۣ�
��3������S��ABE=8�ҳ�kֵ�����P������Ϊ��n��y������A��B��E��PΪ������ı���Ϊƽ���ı����������������������ǣ�����ƽ���ı��ε������Լ�����ϵ�е�����弴�ɵó����ۣ�
��� �⣺��1����y=-$\frac{1}{k}$x2+k=0����x2=k2��
��ã�x1=-k��x2=k��
���A��������-k��0����
��x=0����y=k��
���B��������0��k����
��D��ĺ�����Ϊm��
���E��������m��m������D��������m��0����
��k=3��m=2ʱ��A��-3��0����B��0��3����E��2��2����D��2��0����
S��ABE=$\frac{1}{2}$AO•OB+$\frac{1}{2}$��OB+DE��•OD-$\frac{1}{2}$AD•DE=$\frac{1}{2}$��3��3+$\frac{1}{2}$����3+2����2-$\frac{1}{2}$��3+2����2=$\frac{9}{2}$��
��k=4��m=3ʱ��A��-4��0����B��0��4����E��3��3����D��3��0����
S��ABE=$\frac{1}{2}$AO•OB+$\frac{1}{2}$��OB+DE��•OD-$\frac{1}{2}$AD•DE=$\frac{1}{2}$��4��4+$\frac{1}{2}$����4+3����3-$\frac{1}{2}$��4+3����3=8��
��k=5��m=4ʱ��A��-5��0����B��0��5����E��4��4����D��4��0����
S��ABE=$\frac{1}{2}$AO•OB+$\frac{1}{2}$��OB+DE��•OD-$\frac{1}{2}$AD•DE=$\frac{1}{2}$��5��5+$\frac{1}{2}$����5+4����4-$\frac{1}{2}$��5+4����4=$\frac{25}{2}$��
�ʴ�Ϊ��$\frac{9}{2}$��8��$\frac{25}{2}$��
��2��S��ABE=$\frac{1}{2}{k}^{2}$��
֤�����ɣ�1��֪��A��-k��0����B��0��k����E��m��m����D��m��0����
S��ABE=$\frac{1}{2}$AO•OB+$\frac{1}{2}$��OB+DE��•OD-$\frac{1}{2}$AD•DE=$\frac{1}{2}$k•k+$\frac{1}{2}$��k+m��m-$\frac{1}{2}$��k+m��m=$\frac{1}{2}{k}^{2}$��
��3�����P��������n��y����
��S��ABE=$\frac{1}{2}{k}^{2}$=8��
��k=4��
����A��B��E��PΪ������ı���Ϊƽ���ı���ʱ�������������
�ٵ�AB��EPΪ�Խ���ʱ����Խ��ߵĽ���ΪM����ͼ1��ʾ��
���ı���AEBPΪƽ���ı��Σ�
���Mƽ��AB����Mƽ��EP��
��A��-4��0����B��0��4����E��m��m����P��n��y����
��-4+0=m+n��
��m+n=-4��
��AB��EPΪ�Աߣ��ҵ�P��E�����ʱ���ӳ�ED������P��PN��ED�ڵ�N����ͼ2��ʾ��
���ı���AEBPΪƽ���ı��Σ�
��AB=PE����AB��PE��
��AO=PN��
��A��-4��0����B��0��4����E��m��m����P��n��y����
��0-��-4��=m-n��
��m-n=4��
��AB��EPΪ�Աߣ��ҵ�P��E���Ҳ�ʱ���ӳ�FE������P��PN��FE�ڵ�N����ͼ3��ʾ��
���ı���AEBPΪƽ���ı��Σ�
��AB=PE����AB��PE��
��AO=PN��
��A��-4��0����B��0��4����E��m��m����P��n��y����
��0-��-4��=n-m��
��n-m=4��
���Ͽ�֪������A��B��E��PΪ������ı���Ϊƽ���ı���ʱ��m��n����Ĺ�ϵʽ��m+n=-4��m-n=4��n-m=4��
���� ���⿼���˶��κ�����������Ľ������⡢�����ε������ʽ�Լ�ƽ���ı��ε����ʣ�����Ĺؼ��ǣ���1���ҳ���A��B��E��D�ĵ�����ꣻ��2����k��m��ʾ����A��B��E��D�ĵ�����ꣻ��3�����ƽ���ı��ε������ҳ�m��n֮��Ĺ�ϵ�����������е��⣬��1����2���ѶȲ���3��������������ǣ�����ͬѧ�����ԵĻ�����һ���������������ճ�����ʱҪע����������������������ԡ����������ȫ���ԣ�

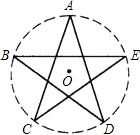 ��ͼΪ�ҹ������ϵ�����ǣ�����A��B��C��D��EΪԲ����ȷֵ㣩����֪AC=a���������ǵ����Բֱ���ɱ�ʾΪ��������
��ͼΪ�ҹ������ϵ�����ǣ�����A��B��C��D��EΪԲ����ȷֵ㣩����֪AC=a���������ǵ����Բֱ���ɱ�ʾΪ��������| A�� | a•sin72�� | B�� | $\frac{a}{tan72��}$ | C�� | $\frac{a}{cos18��}$ | D�� | $\frac{a}{cos36��}$ |
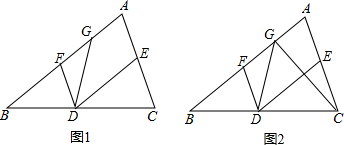
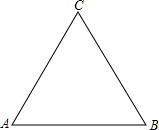 ��֪����ͼ���ȱߡ�ABC��AB=AC=BC=6���뻭����ABC�����Բ��O����Ҫ������ͼ�ۼ���������������Բ�İ뾶r��
��֪����ͼ���ȱߡ�ABC��AB=AC=BC=6���뻭����ABC�����Բ��O����Ҫ������ͼ�ۼ���������������Բ�İ뾶r��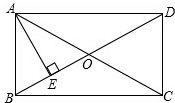 �ھ���ABCD�У��Խ���AC��BD���ڵ�O��AE��BD������ΪE����AEƽ�֡�BAO����DO=2����AB��BC�ij��ȣ�
�ھ���ABCD�У��Խ���AC��BD���ڵ�O��AE��BD������ΪE����AEƽ�֡�BAO����DO=2����AB��BC�ij��ȣ� ��ͼ����֪��1����2������ѡ�1����AD���۹���������AB���2������������λ�ù�ϵ��
��ͼ����֪��1����2������ѡ�1����AD���۹���������AB���2������������λ�ù�ϵ��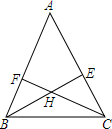 ��֪����ͼ��BE��CF�ǡ�ABC�ĸߣ�H��BE��CF�Ľ��㣬��HB=HC����A=60�㣬��֤����ABCΪ�ȱ������Σ�
��֪����ͼ��BE��CF�ǡ�ABC�ĸߣ�H��BE��CF�Ľ��㣬��HB=HC����A=60�㣬��֤����ABCΪ�ȱ������Σ�