Question

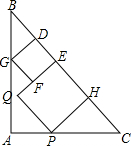在等腰直角三角形ABC中放入两个正方形DEFG和EHPQ，使得DE，EH在斜边BC上，点G，P分别在边AB和AC上，点E，Q始终在△ABC的内部或边上．已知BC长为12，点D是BC上的动点，则这两个正方形面积的最大值为

 

．

Answer 1

考点：相似三角形的判定与性质,二次函数的最值

专题：

分析：设正方形DEFG的边长为x，正方形EHPQ的边长为y，由△ABC是等腰直角三角形，得出x+y=6，两个正方形面积=x²+y²=2（x-3）²+18，利用x的取值范围求出这两个正方形面积的最大值．

解答：解：设正方形DEFG的边长为x，正方形EHPQ的边长为y，
∵△ABC是等腰直角三角形，
∴BD=DG=x，HC=HP=y，
∴x+x+y+y=12，即x+y=6，
∴两个正方形面积=x²+y²=x²+（6-x）²=2x²-12x+36=2（x-3）²+18
如图，

x最大值为4，则最小值为2，
∴2≤x≤4，
∴当x=2或4时，两个正方形面积最大=2（x-3）²+18=20，

点评：本题主要考查了相似三角形的判定与性质及二次函数的最值，解题的关键是找出x的取值范围．