题目内容
把一根长为80cm的绳子剪成两段,并把每一段绳子围成一个正方形.
(1)要使这两个正方形的面积之和等于200cm2,该怎么剪?
(2)这两个正方形面积之和可能等于488cm2吗?
(1)要使这两个正方形的面积之和等于200cm2,该怎么剪?
(2)这两个正方形面积之和可能等于488cm2吗?
考点:一元二次方程的应用
专题:几何图形问题
分析:(1)利用正方形的性质表示出边长进而得出等式求出即可;
(2)利用正方形的性质表示出边长进而得出等式,进而利用根的判别式求出即可.
(2)利用正方形的性质表示出边长进而得出等式,进而利用根的判别式求出即可.
解答:解:设剪成的一段为xcm,则另一段就为(80-x)cm,
由题意得(
)2+(
)2=200;
解得:x1=x2=40.
答:将该绳子从中间截开;
(2)设剪成的较短的这段为mcm,较长的这段就为(80-m)cm,
由题意得:(
)2+(
)2=488,
变形为:m2-80m-704=0,
∵△=6400+2816=9216>0,
∴原方程有解.
答:这两个正方形的面积之和可能等于488cm2.
由题意得(
| x |
| 4 |
| 80-x |
| 4 |
解得:x1=x2=40.
答:将该绳子从中间截开;
(2)设剪成的较短的这段为mcm,较长的这段就为(80-m)cm,
由题意得:(
| m |
| 4 |
| 80-m |
| 4 |
变形为:m2-80m-704=0,
∵△=6400+2816=9216>0,
∴原方程有解.
答:这两个正方形的面积之和可能等于488cm2.
点评:此题主要考查了一元二次方程的应用,根据正方形的性质表示出正方形的边长是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,?ABCD中,E、F分别是BC和AD边上的点,且BE=DF.试判断两条线段AE与CF有怎样的数量及位置关系?并说明理由.
如图,?ABCD中,E、F分别是BC和AD边上的点,且BE=DF.试判断两条线段AE与CF有怎样的数量及位置关系?并说明理由. 我们知道在中国象棋马走日象走田,如图,假设一匹马经过A、B两点走到点C,请问点A、B、C是否在一条直线上?请你建立适当的坐标系并用学过的数学知识说明理由.
我们知道在中国象棋马走日象走田,如图,假设一匹马经过A、B两点走到点C,请问点A、B、C是否在一条直线上?请你建立适当的坐标系并用学过的数学知识说明理由. 对于平面直角坐标系xOy中的点P(a,b),若点P′的坐标为(
对于平面直角坐标系xOy中的点P(a,b),若点P′的坐标为(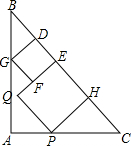 在等腰直角三角形ABC中放入两个正方形DEFG和EHPQ,使得DE,EH在斜边BC上,点G,P分别在边AB和AC上,点E,Q始终在△ABC的内部或边上.已知BC长为12,点D是BC上的动点,则这两个正方形面积的最大值为
在等腰直角三角形ABC中放入两个正方形DEFG和EHPQ,使得DE,EH在斜边BC上,点G,P分别在边AB和AC上,点E,Q始终在△ABC的内部或边上.已知BC长为12,点D是BC上的动点,则这两个正方形面积的最大值为