题目内容
 如图,?ABCD的面积为16,对角线交于点O;以AB、AO为邻边作?AOC1B,对角线交于点O1;以AB、AO1为邻边作?AO1C2B,对角线交于点O2;…;依此类推.则?AOC1B的面积为
如图,?ABCD的面积为16,对角线交于点O;以AB、AO为邻边作?AOC1B,对角线交于点O1;以AB、AO1为邻边作?AO1C2B,对角线交于点O2;…;依此类推.则?AOC1B的面积为考点:平行四边形的性质
专题:规律型
分析:根据平行四边形的性质得出O1A=O1C1,O1B=O1O,求出SAO1B=
S△ABC1=
S?ABCD=4cm2,求出四边形ABC1O是菱形,推出AC1=2O1A,O1B=2O1O2=2O2B,AC1⊥BO1,平行四边形ABC1O的面积是AC1×BO1=8cm2,推出△ABO2的面积是2cm2,同理平行四边形ABC2O2的面积是4cm2,平行四边形ABC3O3的面积是2cm2,平行四边形ABC4O4的面积是1cm2,平行四边形ABC5D5的面积是
cm2,进而得到问题的规律,所以?AOnCn+1B的面积可求.
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
解答: 解:∵四边形ABCD是平行四边形,
解:∵四边形ABCD是平行四边形,
∴O1A=O1C1,O1B=O1O,
∴SAO1B=
S△ABC1=
S?ABCD=4cm2,
∵四边形ABC1O1是平行四边形,O1A=O1B,
∴四边形ABC1O是菱形,
∴AC1=2O2A,O1B=2O1O2=2O2B,AC1⊥BO1,
∴平行四边形ABC1O1的面积是AC1×BO1=×2AO2×BO1=2×AO2×BO1=2×4cm2=8cm2,
∴△ABO2的面积=2cm2,
同理平行四边形ABC2O2的面积是4cm2,
平行四边形ABC3O3的面积是2cm2,
平行四边形ABC4O4的面积是1cm2,
平行四边形ABC5D5的面积是
cm2,
…以此类推?AOnCn+1B的面积为:
或
故答案为:8;
;
或
.
 解:∵四边形ABCD是平行四边形,
解:∵四边形ABCD是平行四边形,∴O1A=O1C1,O1B=O1O,
∴SAO1B=
| 1 |
| 2 |
| 1 |
| 4 |
∵四边形ABC1O1是平行四边形,O1A=O1B,
∴四边形ABC1O是菱形,
∴AC1=2O2A,O1B=2O1O2=2O2B,AC1⊥BO1,
∴平行四边形ABC1O1的面积是AC1×BO1=×2AO2×BO1=2×AO2×BO1=2×4cm2=8cm2,
∴△ABO2的面积=2cm2,
同理平行四边形ABC2O2的面积是4cm2,
平行四边形ABC3O3的面积是2cm2,
平行四边形ABC4O4的面积是1cm2,
平行四边形ABC5D5的面积是
| 1 |
| 2 |
…以此类推?AOnCn+1B的面积为:
| 8 |
| 2n |
| 16 |
| 2n+1 |
故答案为:8;
| 1 |
| 2 |
| 8 |
| 2n |
| 16 |
| 2n+1 |
点评:本题考查了平行四边形性质,菱形的性质和判定,三角形的面积等知识点,此题的关键是能根据求出的结果得出规律,注意:等底等高的三角形的面积相等.

练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案
相关题目
下列运算一定正确的是( )
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
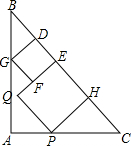 在等腰直角三角形ABC中放入两个正方形DEFG和EHPQ,使得DE,EH在斜边BC上,点G,P分别在边AB和AC上,点E,Q始终在△ABC的内部或边上.已知BC长为12,点D是BC上的动点,则这两个正方形面积的最大值为
在等腰直角三角形ABC中放入两个正方形DEFG和EHPQ,使得DE,EH在斜边BC上,点G,P分别在边AB和AC上,点E,Q始终在△ABC的内部或边上.已知BC长为12,点D是BC上的动点,则这两个正方形面积的最大值为 如图,AC=BC,∠ACD=120°,则∠A的度数为
如图,AC=BC,∠ACD=120°,则∠A的度数为