题目内容

已知x2+y2-6x+4y+20，则它的最小值是
 
，此时x=
 
y=
 
．
考点：配方法的应用,非负数的性质：偶次方
专题：
分析：原式配方变形后，利用非负数的性质求出最小值，以及此时x与y的值．
解答：解：x2+y2-6x+4y+20=（x-3）2+（y+2）2+7≥7，
当x-3=0，y+2=0，即x=3，y=-2时，最小值是7．
故答案为：7；3；-2
点评：此题考查了配方法的应用，以及非负数的性质，熟练掌握完全平方公式是解本题的关键．
练习册系列答案
相关题目
对于平面直角坐标系xOy中的点P（a，b），若点P′的坐标为（a+
b
k
，ka+b）（其中k为常数，且k≠0），则称点P′为点P的“k属派生点”．
例如：P（1，4）的“2属派生点”为P′（1+
4
2
，2×1+4），即P′（3，6）．
（1）①点P（-1，-2）的“2属派生点”P′的坐标为
 
；
②若点P的“k属派生点”P′的坐标为（3，3），请写出一个符合条件的点P的坐标
 
；
（2）若点P在x轴的正半轴上，点P的“k属派生点”为P′点，且△OPP′为等腰直角三角形，求k的值．
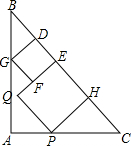在等腰直角三角形ABC中放入两个正方形DEFG和EHPQ，使得DE，EH在斜边BC上，点G，P分别在边AB和AC上，点E，Q始终在△ABC的内部或边上．已知BC长为12，点D是BC上的动点，则这两个正方形面积的最大值为
 
．
因式分解：-2x2+4x+6=
 
．
若代数式x2-12x+a2可以分解为（x-b）2，则a=
 
，b=
 
．
已知△ABC的面积为24，四边形DEFG是它的内接矩形，则矩形DEFG的面积最大值是
 
．
如图，AC=BC，∠ACD=120°，则∠A的度数为
 
．
如图，观察该三角形数阵，按此规律下去，第n行的第一个数是
 
．
已知菱形ABCD的两条对角线AC、BD的长分别为6和8，则边长CD的长为（　　）
A、6B、8C、14D、5

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网