题目内容
20. 如图,在直升机的镜头下,观测A处的俯角为30°,B处的俯角为45°.如果此时直升机镜头C处的高度CD为200米,点A、D、B在同一直线上,则AB两点的距离是200($\sqrt{3}$+1)米.
如图,在直升机的镜头下,观测A处的俯角为30°,B处的俯角为45°.如果此时直升机镜头C处的高度CD为200米,点A、D、B在同一直线上,则AB两点的距离是200($\sqrt{3}$+1)米.
分析 分别在RT△ADC,RT△BDC中求出AD,BD即可解决问题.
解答 解: 在RT△ACD中,∵∠ADC=90°,CD=200,∠A=30°,
在RT△ACD中,∵∠ADC=90°,CD=200,∠A=30°,
∴tanA=$\frac{CD}{AD}$,
∴AD=200$\sqrt{3}$,
在RT△BDC中,∵∠CDB=90°,∠B=∠DCB=45°,
∴CD=DB=200,
∴AB=200$\sqrt{3}$+200=200($\sqrt{3}$+1)米.
故答案为200($\sqrt{3}+1$)米.
点评 本题考查解直角三角形的应用、俯角俯角、三角函数等知识,解题的关键是记住三角函数的定义,以及特殊三角形的边角关系,属于中考常考题型.

练习册系列答案
相关题目
11. 如图,已知A是反比例函数y=$\frac{k}{x}$图象上的一点,过点A向x轴作垂线交x轴于点B,在点A从左往右移动的过程中,△ABO的面积将( )
如图,已知A是反比例函数y=$\frac{k}{x}$图象上的一点,过点A向x轴作垂线交x轴于点B,在点A从左往右移动的过程中,△ABO的面积将( )
 如图,已知A是反比例函数y=$\frac{k}{x}$图象上的一点,过点A向x轴作垂线交x轴于点B,在点A从左往右移动的过程中,△ABO的面积将( )
如图,已知A是反比例函数y=$\frac{k}{x}$图象上的一点,过点A向x轴作垂线交x轴于点B,在点A从左往右移动的过程中,△ABO的面积将( )| A. | 越来越大 | B. | 越来越小 | C. | 先变大,后变小 | D. | 不变 |
9.下列选项中,可以用来说明命题“两个锐角的和是锐角”是假命题的反例的是( )
| A. | ∠A=30°,∠B=40° | B. | ∠A=30°,∠B=110° | C. | ∠A=30°,∠B=70° | D. | ∠A=30°,∠B=90° |

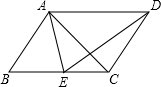 如图,在?ABCD中,E为BC边上一点,且AB=AE,若AE平分∠DAB,∠EAC=25°,则∠AED的度数是85度.
如图,在?ABCD中,E为BC边上一点,且AB=AE,若AE平分∠DAB,∠EAC=25°,则∠AED的度数是85度.