题目内容
12.2015年中考之后,某中学想了解本校九年级学生数学成绩状况,随机抽取了部分学生的测试成绩作为样本进行分析,绘制成了如下两幅不完整的统计图,请根据图中所给信息,解答下列问题:(1)请将表示成绩类别为“中”的条形统计图补充完整;
(2)在扇形统计图中,表示成绩类别为“优”的扇形所对应的圆心角是72度;
(3)该学校九年级共有800人参加了中考,估算该校九年级共有多少名学生的数学成绩可以达到优秀?

分析 (1)结合条形统计图和扇形统计图,先用成绩类别为“良”的人数÷44%,得被抽取的学生总数,再用被抽取的学生总数×成绩类别为“中”的人数所占的百分比求得成绩类别为“中”的人数,从而补全条形统计图.
(2)成绩类别为“优”的扇形所占的百分比=成绩类别为“优”的人数÷被抽取的学生总数,它所对应的圆心角的度数=360°×成绩类别为“优”的扇形所占的百分比.
(3)该校九年级学生的数学成绩达到优秀的人数=800×成绩类别为“优”的学生所占的百分比.
解答 解:(1)本次抽查的学生一共有22÷44%=50(人),
则成绩类别为“中”的学生数为:50×20%=10(人),补全条形统计图如图:
(2)成绩类别为“优”的扇形所对应的圆心角是$\frac{10}{50}$×360°=72°;
故答案为:72.
(3)800×$\frac{10}{50}$=160(人),
答:估算该校九年级共有160名学生的数学成绩可以达到优秀.
点评 本题考查的是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.

练习册系列答案
相关题目
20. 如图,在直升机的镜头下,观测A处的俯角为30°,B处的俯角为45°.如果此时直升机镜头C处的高度CD为200米,点A、D、B在同一直线上,则AB两点的距离是200($\sqrt{3}$+1)米.
如图,在直升机的镜头下,观测A处的俯角为30°,B处的俯角为45°.如果此时直升机镜头C处的高度CD为200米,点A、D、B在同一直线上,则AB两点的距离是200($\sqrt{3}$+1)米.
 如图,在直升机的镜头下,观测A处的俯角为30°,B处的俯角为45°.如果此时直升机镜头C处的高度CD为200米,点A、D、B在同一直线上,则AB两点的距离是200($\sqrt{3}$+1)米.
如图,在直升机的镜头下,观测A处的俯角为30°,B处的俯角为45°.如果此时直升机镜头C处的高度CD为200米,点A、D、B在同一直线上,则AB两点的距离是200($\sqrt{3}$+1)米.
7. 为了美观,在加工太阳镜时将下半部分轮廓制作成抛物线的形状(如图所示),对应的两条抛物线关于y轴对称,AE∥x轴,AB=4cm,最低点C在x轴上,高CH=1cm,BD=2cm,则右轮廓DFE所在抛物线的解析式为( )
为了美观,在加工太阳镜时将下半部分轮廓制作成抛物线的形状(如图所示),对应的两条抛物线关于y轴对称,AE∥x轴,AB=4cm,最低点C在x轴上,高CH=1cm,BD=2cm,则右轮廓DFE所在抛物线的解析式为( )
 为了美观,在加工太阳镜时将下半部分轮廓制作成抛物线的形状(如图所示),对应的两条抛物线关于y轴对称,AE∥x轴,AB=4cm,最低点C在x轴上,高CH=1cm,BD=2cm,则右轮廓DFE所在抛物线的解析式为( )
为了美观,在加工太阳镜时将下半部分轮廓制作成抛物线的形状(如图所示),对应的两条抛物线关于y轴对称,AE∥x轴,AB=4cm,最低点C在x轴上,高CH=1cm,BD=2cm,则右轮廓DFE所在抛物线的解析式为( )| A. | y=$\frac{1}{4}$(x+3)2 | B. | y=$\frac{1}{4}$(x-3)2 | C. | y=-$\frac{1}{4}$(x+3)2 | D. | y=-$\frac{1}{4}$(x-3)2 |
 某厂家生产并销售某种产品,假设销售量与产量相等,如图中的折线ABD,线段CD分别表示该产品每千克生产成本y1(单位:元),销售价y2(单位:元)与产量x(单位:kg)之间的函数关系.
某厂家生产并销售某种产品,假设销售量与产量相等,如图中的折线ABD,线段CD分别表示该产品每千克生产成本y1(单位:元),销售价y2(单位:元)与产量x(单位:kg)之间的函数关系. 如图,D、E是以AB为直径的⊙O上两点,且∠AED=45°.
如图,D、E是以AB为直径的⊙O上两点,且∠AED=45°.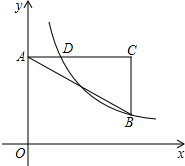 如图在直角坐标系中,点A在y轴正半轴上,AC∥x轴,点B,C的横坐标都是3,且BC=2,点D在AC上且横坐标为1,若反比例函数y=$\frac{k}{x}$(x>0)图象象经过点B,D,求k的值.
如图在直角坐标系中,点A在y轴正半轴上,AC∥x轴,点B,C的横坐标都是3,且BC=2,点D在AC上且横坐标为1,若反比例函数y=$\frac{k}{x}$(x>0)图象象经过点B,D,求k的值. 如图,桌子上放着一个长方体的茶叶盒和一个圆柱形的水杯,则它的俯视图是( )
如图,桌子上放着一个长方体的茶叶盒和一个圆柱形的水杯,则它的俯视图是( )



 如图,在?ABCD中,E、F为对角线AC上两点,且DE∥BF,求证:△AFB≌△CED.
如图,在?ABCD中,E、F为对角线AC上两点,且DE∥BF,求证:△AFB≌△CED.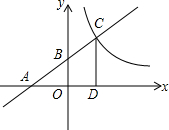 已知函数y1=$\frac{2}{3}$x+2的图象分别与坐标轴相交于A,B两点(如图所示),与反比例函数y2=$\frac{k}{x}$(x>0)的图象相交于C点.
已知函数y1=$\frac{2}{3}$x+2的图象分别与坐标轴相交于A,B两点(如图所示),与反比例函数y2=$\frac{k}{x}$(x>0)的图象相交于C点.