题目内容
甲、乙两公司各为希望工程捐款20000元，已知乙公司比甲公司人均多捐20元，且乙公司的人数是甲公司人数的
，问甲、乙两公司人均捐款各为多少元．
| 4 |
| 5 |
考点：分式方程的应用
专题：
分析：本题的等量关系是：甲公司的人均捐款+20=乙公司的人均捐款．根据这个等量关系可得出方程求解．
解答：解：设甲公司人均捐款x元，则乙公司人均捐款x+20元，
根据题意得：
×
=
解得：x=80
经检验x=80是原方程的根，
故x+20=80+20=100元，
答：甲公司人均捐款80元，乙公司人均捐款100元．
根据题意得：
| 20000 |
| x |
| 4 |
| 5 |
| 20000 |
| x+20 |
解得：x=80
经检验x=80是原方程的根，
故x+20=80+20=100元，
答：甲公司人均捐款80元，乙公司人均捐款100元．
点评：本题考查了分式方程的应用，解题关键是要读懂题目的意思，根据题目给出的条件，找出合适的等量关系，列出方程，再求解．
练习册系列答案
阅读快车系列答案
相关题目
已知a-
=1，且
=-
，则x的值等于（ ）
| 1 |
| a |
| 2a4-3a2x+2 |
| a3+2a2x-a |
| 12 |
| 13 |
| A、6 | B、7 | C、8 | D、9 |
已知24-n•42n+1=8-n，则n的值为（ ）
| A、n=-3 | B、n=-2 |
| C、n=-1 | D、n=0 |
已知反比例函数y=
的图象，在每一个象限内，y的值随x值的增大而增大，则该函数图象分布在（ ）
| k |
| x |
| A、第一、二象限 |
| B、第一、三象限 |
| C、第二、四象限 |
| D、第三、四象限 |
如图，AD平分∠EAC，且AD∥BC，请说明∠B=∠C的理由．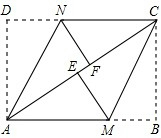
已知：如图，在矩形ABCD中，把∠B、∠D分别翻折，使点B、D分别落在对角线BC上的点E、F处，折痕分别为CM、AN．
