Question

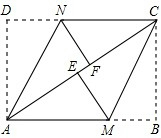已知：如图，在矩形ABCD中，把∠B、∠D分别翻折，使点B、D分别落在对角线BC上的点E、F处，折痕分别为CM、AN．
（1）求证：△ADN≌△CBM．
（2）请连接MF、NE，证明四边形MFNE是平行四边形，四边形MFNE是菱形吗？请说明理由．

Answer 1

考点：翻折变换（折叠问题）,全等三角形的判定与性质,平行四边形的判定,菱形的判定,矩形的性质

专题：

分析：（1）根据折叠的性质得出∠DAN=∠NAC，∠BCM=∠ACM，从而根据AD∥BC可得出∠DAN=∠BCM，从而即可判断出△ADN≌△CBM．
（2）连接NE、MF，根据（1）的结论可得出NF=ME，再由∠NFE=∠MEF可判断出NF∥ME，在直角三角形EMF中，FM为斜边，EM为直角边，可判断四边形MFNE不是菱形．

解答：（1）证明：∵四边形ABCD是矩形，
∴∠D=∠B，AD=BC，AD∥BC．
∴∠DAC=∠BCA．
又由翻折的性质，得∠DAN=∠NAF，∠ECM=∠BCM，
∴∠DAN=∠BCM．
在△AND和△CBM中，

∠D=∠B AD=BC ∠DAN=∠BCM

，
△AND≌△CBM（ASA）．

（2）证明：连接NE、MF，

∵△AND≌△CBM，
∴DN=BM．
又由翻折的性质，得DN=FN，BM=EM，
∴FN=EM．
又∵∠NFA=∠ACD+∠CNF=∠BAC+∠EMA=∠MEC，
∴FN∥EM．
∴四边形MFNE是平行四边形．
四边形MFNE不是菱形，理由如下：
由翻折的性质，得∠CEM=∠B=90°，
∴在△EMF中，∠FEM＞∠EFM．
∴FM＞EM．
∴四边形MFNE不是菱形．

点评：本题主要考查翻折变换的知识点，涉及全等三角形的判定与性质、平行四边形、菱形的判定，以及矩形的性质的知识．