题目内容
求证:两个三角形有两条边对应相等,如果所夹的角不相等,那么夹角所对的边也不相等.
考点:反证法
专题:证明题
分析:首先写出已知与求证,再利用反证法的证明步骤,从结论的反面出发假设求证结论不成立,进而得出矛盾,从而证明原命题正确.
解答: 已知:AB=A′B′,BC=B′C′,∠B≠∠B′,
已知:AB=A′B′,BC=B′C′,∠B≠∠B′,
求证:AC≠A′C′.
证明:假设AC=A′C′,
在△ABC和△A′B′C′中
,
∴△ABC≌△A′B′C′(SSS),
∴∠B=∠B′,
∴与已知,∠B≠∠B′矛盾,则假设不成立,
∴AC≠A′C′.
 已知:AB=A′B′,BC=B′C′,∠B≠∠B′,
已知:AB=A′B′,BC=B′C′,∠B≠∠B′,求证:AC≠A′C′.
证明:假设AC=A′C′,
在△ABC和△A′B′C′中
|
∴△ABC≌△A′B′C′(SSS),
∴∠B=∠B′,
∴与已知,∠B≠∠B′矛盾,则假设不成立,
∴AC≠A′C′.
点评:此题考查反证法的定义:从否定命题的结论入手,并把对命题结论的否定作为推理的已知条件,进行正确的逻辑推理,使之得到与已知条件、已知公理、定理、法则或者已经证明为正确的命题等相矛,矛盾的原因是假设不成立,所以肯定了命题的结论,从而使命题获得了证明.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,三条直线AB,CD,EF交于一点,若∠1=30°,∠2=70°,求∠3的度数.
如图,三条直线AB,CD,EF交于一点,若∠1=30°,∠2=70°,求∠3的度数.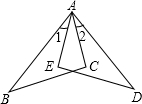 如图,已知AB=AD,AC=AE,∠1=∠2,求证:BC=DE.
如图,已知AB=AD,AC=AE,∠1=∠2,求证:BC=DE.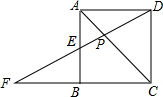 如图,正方形ABCD中,F是CB延长线上的一点,DF交AB于E,交对角线AC于P,如PE=2,EF=3.求PD的长.
如图,正方形ABCD中,F是CB延长线上的一点,DF交AB于E,交对角线AC于P,如PE=2,EF=3.求PD的长. 如图,在等腰三角形ABC中,∠BAC=120°,D为BC的中点,DE⊥AB于E,求证:AE=
如图,在等腰三角形ABC中,∠BAC=120°,D为BC的中点,DE⊥AB于E,求证:AE= 如图,∠C=90°,若△ACD的周长为7cm,DE为AB边的垂直平分线,则AC+BC=
如图,∠C=90°,若△ACD的周长为7cm,DE为AB边的垂直平分线,则AC+BC=