题目内容
4.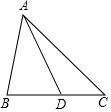 如图,△ABC中,点D在线段BC上,且△ABC∽△DBA,则下列结论一定正确的是( )
如图,△ABC中,点D在线段BC上,且△ABC∽△DBA,则下列结论一定正确的是( )| A. | AB2=BC•BD | B. | AB2=AC•BD | C. | AB•AD=BD•BC | D. | AB•AC=BC•BD |
分析 根据相似三角形的性质列出比例式,判断即可.
解答 解:∵△ABC∽△DBA,
∴$\frac{AB}{BD}$=$\frac{BC}{AB}$,
∴AB2=BC•BD,A正确;
$\frac{AB}{BD}$=$\frac{AC}{AD}$,
∴AB•AD=AC•BD,B错误,C错误,D错误;
故选:A.
点评 本题考查的是相似三角形的性质,掌握相似三角形的对应角相等,对应边的比相等是解题的关键.

练习册系列答案
相关题目
9.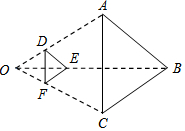 如图,以点O为位似中心,将△ABC缩小后得到△DEF,已知OD=1,OA=3.若△DEF的面积为S,则△ABC的面积为( )
如图,以点O为位似中心,将△ABC缩小后得到△DEF,已知OD=1,OA=3.若△DEF的面积为S,则△ABC的面积为( )
 如图,以点O为位似中心,将△ABC缩小后得到△DEF,已知OD=1,OA=3.若△DEF的面积为S,则△ABC的面积为( )
如图,以点O为位似中心,将△ABC缩小后得到△DEF,已知OD=1,OA=3.若△DEF的面积为S,则△ABC的面积为( )| A. | 2S | B. | 3S | C. | 4S | D. | 9S |
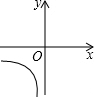 如图是反比例函数y=$\frac{k+5}{x}$的图象的一支,根据图象回答下列问题:
如图是反比例函数y=$\frac{k+5}{x}$的图象的一支,根据图象回答下列问题: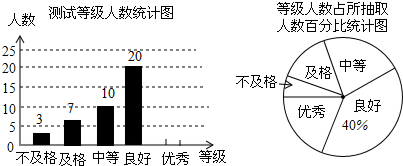
 如图OP=1,过P作PP1⊥OP且PP1=1,得OP1=$\sqrt{2}$,再过点P1作P1P2⊥OP1且P1P2=1,连接OP2,得OP2=$\sqrt{3}$;又过点P2作P2P3⊥OP2且P2P3=1,得OP3=2;依此法继续作下去,得OP12+OP22+OP32+OP42+…+OPn2=$\frac{n(n+3)}{2}$.
如图OP=1,过P作PP1⊥OP且PP1=1,得OP1=$\sqrt{2}$,再过点P1作P1P2⊥OP1且P1P2=1,连接OP2,得OP2=$\sqrt{3}$;又过点P2作P2P3⊥OP2且P2P3=1,得OP3=2;依此法继续作下去,得OP12+OP22+OP32+OP42+…+OPn2=$\frac{n(n+3)}{2}$.