Question

如图，在等腰△ABC中，∠BAC=120°，DE是AC的垂直平分线，线段DE=1cm，则BD的长为 （ ）

．

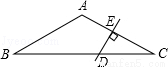A．6cm B．8cm C .3cm D．4cm

Answer 1

D

【解析】

过A作AF∥DE交BD于F，则DE是△CAF的中位线，∴AF=2DE=2，又∵DE⊥AC，∠C=30°，∴FD=CD=2DE=2，在△AFB中，∠1=∠B=30°，∴BF=AF=2，∴BD=4．

考点：线段垂直平分线的性质；含30度角的直角三角形；三角形中位线定理．