Question

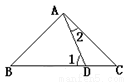
如图,已知: AD是BC上的中线 ,且DF=DE．求证:BE∥CF．（8分）

Answer 1

证明：∵AD是BC上的中线，

∴BD=DC．

又∵DF=DE（已知），

∠BDE=∠CDF（对顶角相等），

∴△BED≌△CFD（SAS）．

∴∠E=∠CFD（全等三角形的对应角相等）．

∴CF∥BE（内错角相等，两直线平行）．

【解析】

试题分析：欲证BE∥CF，需先证得∠EBC=∠FCD或∠E=∠CFD，那么关键是证△BED≌△CFD；这两个三角形中，已知的条件有：BD=DC，DE=DF，而对顶角∠BDE=∠CDF，根据SAS即可证得这两个三角形全等，由此可得出所证的结论．

考点：全等三角形的判定与性质、平行线的判定