题目内容
10.若30°<α<β<90°,则$\sqrt{{{({cosβ-cosα})}^2}}$-$|{cosβ-\frac{{\sqrt{3}}}{2}}|$+|1-cosα|=1-$\frac{\sqrt{3}}{2}$.分析 根据锐角三角函数的增减性判断出cosβ与cosα的大小、cosβ与$\frac{\sqrt{3}}{2}$的大小,然后化简计算即可.
解答 解:∵30°<α<β<90°,
∴cosβ<cosα,cosβ<$\frac{\sqrt{3}}{2}$.
∴原式=|cosβ-cosα|+cosβ-$\frac{\sqrt{3}}{2}$+1-cosα=-cosβ+cosα+cosβ-$\frac{\sqrt{3}}{2}$+1-cosα=1-$\frac{\sqrt{3}}{2}$.
故答案为:1-$\frac{\sqrt{3}}{2}$.
点评 本题主要考查的是二次根式的化简、锐角三角函数的增减性,掌握锐角三角函数的增减性是解题的关键.

练习册系列答案
相关题目
15.一个点到圆的最大距离为11,最小距离为5,则圆的半径为( )
| A. | 16或6 | B. | 3或8 | C. | 3 | D. | 8 |
2.已知一个物体由x个相同的正方体堆成,它的主视图和左视图如图所示,那么x的最小值是( )


| A. | 5 | B. | 4 | C. | 3 | D. | 2 |
 如图,已知A、D、E三点共线.C、B、F三点共线,AB=CD,AD=CB,DE=BF,那么BE与DF之间有什么数量关系?请说明理由.
如图,已知A、D、E三点共线.C、B、F三点共线,AB=CD,AD=CB,DE=BF,那么BE与DF之间有什么数量关系?请说明理由.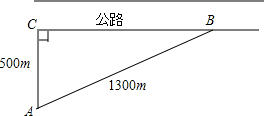 我方侦查员小王在距离东西向500米处公路侦查,发现一辆敌方汽车在公路上疾驶.他赶紧拿出红外测距仪,测得汽车与他相距500米,30秒后,汽车与他相距1300米,请你帮小王计算敌方汽车的速度吗?
我方侦查员小王在距离东西向500米处公路侦查,发现一辆敌方汽车在公路上疾驶.他赶紧拿出红外测距仪,测得汽车与他相距500米,30秒后,汽车与他相距1300米,请你帮小王计算敌方汽车的速度吗?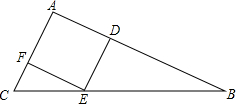 △ABC的边AB=6,AC=4,若菱形DEFA内接于△ABC,则菱形的边长为2.4.
△ABC的边AB=6,AC=4,若菱形DEFA内接于△ABC,则菱形的边长为2.4.