��Ŀ����
��ͼ����ͼ��������y=x2+bx+c��x�ύ�ڵ�A�͵�B��4��0������y�ύ�ڵ�C��0��4��.
��1���������ߵĽ���ʽ��
��2������M����������x���·��Ķ��㣬����M��MN��y�ύֱ��BC�ڵ�N���߶�MN�����ֵ����3���ڣ�2���������£���MNȡ�����ֵʱ���������ߵĶԳ���l���Ƿ���ڵ�Pʹ��PBN�ǵ��������Σ������ڣ���ֱ��д�����е�P�����ꣻ�������ڣ���˵������.
��ϰ��ϵ�д�
�����Ŀ


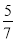 ����n��ֵ��
����n��ֵ��