题目内容
6.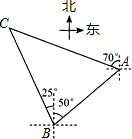 如图,小岛A在港口B的北偏东50°方向,小岛C在港口B的北偏西25°方向,一艘轮船以每小时20海里的速度从港口B出发向小岛A航行,经过5小时到达小岛A,这时测得小岛C在小岛A的北偏西70°方向,求小岛A距离小岛C有多少海里?(最后结果精确到1海里,参考数据:$\sqrt{2}$≈1.1414,$\sqrt{3}$≈1.732)
如图,小岛A在港口B的北偏东50°方向,小岛C在港口B的北偏西25°方向,一艘轮船以每小时20海里的速度从港口B出发向小岛A航行,经过5小时到达小岛A,这时测得小岛C在小岛A的北偏西70°方向,求小岛A距离小岛C有多少海里?(最后结果精确到1海里,参考数据:$\sqrt{2}$≈1.1414,$\sqrt{3}$≈1.732)
分析 过点B作BD⊥AC,垂足为点D,根据题意求出∠ABC和∠BAC的度数以及AB的长,再求出AD和BD的长,结合CD=BD,即可求出AC的长.
解答 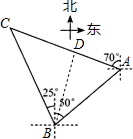 解:由题意得,∠ABC=25°+50°=75°,∠BAC=180°-70°-50°=60°,
解:由题意得,∠ABC=25°+50°=75°,∠BAC=180°-70°-50°=60°,
∴在△ABC中,∠C=45°,
过点B作BD⊥AC,垂足为点D,
∵AB=20×5=100,
在Rt△ABD中,∠BAD=60°,
∴BD=ABsin60°=100×$\frac{\sqrt{3}}{2}$=50$\sqrt{3}$,
∴AD=ABcos60°=100×$\frac{1}{2}$=50,
在Rt△BCD中,∠C=45°,
∴CD=BD=50$\sqrt{3}$,
∴AC=AD+CD=50+50$\sqrt{3}$≈137(海里),
答:小岛A距离小岛C约是137海里.
点评 此题考查了解直角三角形的应用-方向角问题的知识,解答此类题目的关键是构造出直角三角形,利用解直角三角形的相关知识解答,此题难度不大.

练习册系列答案
相关题目
1.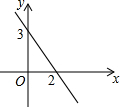 一次函数y=kx-k(k≠0)的图象如图所示,若y>0,则x的取值范围是( )
一次函数y=kx-k(k≠0)的图象如图所示,若y>0,则x的取值范围是( )
 一次函数y=kx-k(k≠0)的图象如图所示,若y>0,则x的取值范围是( )
一次函数y=kx-k(k≠0)的图象如图所示,若y>0,则x的取值范围是( )| A. | x<0 | B. | x>0 | C. | x>2 | D. | x<2 |
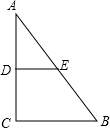 如图,在Rt△ABC中,∠C=90°,D是AC上一个动点,点E在AB上,DE∥BC,已知:AB=5,BC=3.设CD长为x,四边形CDEB面积为y,求y关于x的函数解析式,并写出定义域.
如图,在Rt△ABC中,∠C=90°,D是AC上一个动点,点E在AB上,DE∥BC,已知:AB=5,BC=3.设CD长为x,四边形CDEB面积为y,求y关于x的函数解析式,并写出定义域.