题目内容
17.计算:$\frac{(\sqrt{3}+\sqrt{5})(\sqrt{5}+\sqrt{7})}{\sqrt{3}+2\sqrt{5}+\sqrt{7}}$.分析 首先求出原式的倒数的值,进而得出答案.
解答 解:∵$\frac{\sqrt{3}+\sqrt{5}+\sqrt{5}+\sqrt{7}}{(\sqrt{3}+\sqrt{5})(\sqrt{5}+\sqrt{7})}$
=$\frac{1}{\sqrt{5}+\sqrt{7}}$+$\frac{1}{\sqrt{3}+\sqrt{5}}$
=$\frac{\sqrt{5}-\sqrt{7}}{-2}$+$\frac{\sqrt{3}-\sqrt{5}}{-2}$
=$\frac{\sqrt{3}-\sqrt{7}}{-2}$,
∴原式=$\frac{-2}{\sqrt{3}-\sqrt{7}}$=$\frac{-2(\sqrt{3}+\sqrt{7})}{(\sqrt{3}-\sqrt{7})(\sqrt{3}+\sqrt{7})}$=$\frac{\sqrt{3}+\sqrt{7}}{2}$.
点评 此题主要考查了二次根式的混合运算,正确利用二次根式的性质求出是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
12.若a>b,则下列不等式变形正确的是( )
| A. | a+5<b+5 | B. | $\frac{a}{3}$<$\frac{b}{3}$ | C. | -4a>-4b | D. | 3a-2>3b-2 |
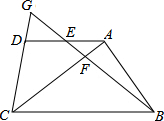 如图,在梯形ABCD中,AD∥BC,点E是边AD的中点,连接BE,交AC于点F,BE的延长线交CD的延长线于点G.
如图,在梯形ABCD中,AD∥BC,点E是边AD的中点,连接BE,交AC于点F,BE的延长线交CD的延长线于点G.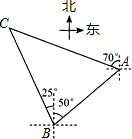 如图,小岛A在港口B的北偏东50°方向,小岛C在港口B的北偏西25°方向,一艘轮船以每小时20海里的速度从港口B出发向小岛A航行,经过5小时到达小岛A,这时测得小岛C在小岛A的北偏西70°方向,求小岛A距离小岛C有多少海里?(最后结果精确到1海里,参考数据:$\sqrt{2}$≈1.1414,$\sqrt{3}$≈1.732)
如图,小岛A在港口B的北偏东50°方向,小岛C在港口B的北偏西25°方向,一艘轮船以每小时20海里的速度从港口B出发向小岛A航行,经过5小时到达小岛A,这时测得小岛C在小岛A的北偏西70°方向,求小岛A距离小岛C有多少海里?(最后结果精确到1海里,参考数据:$\sqrt{2}$≈1.1414,$\sqrt{3}$≈1.732)