题目内容
1. 如图,已知四边形ABCD内接于半径为4的⊙O中,且∠C=2∠A,则BD=4$\sqrt{3}$.
如图,已知四边形ABCD内接于半径为4的⊙O中,且∠C=2∠A,则BD=4$\sqrt{3}$.
分析 连接OD、OB,过点O作OF⊥BD,垂足为F,由垂径定理可知DF=BF,∠DOF=∠BOF,再由圆内接四边形的性质求出∠A的度数,故可得出∠BOD的度数,再由锐角三角函数的定义求出BF的长,进而可得出结论.
解答 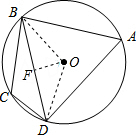 解:连接OD、OB,过点O作OF⊥BD,垂足为F,
解:连接OD、OB,过点O作OF⊥BD,垂足为F,
∵OF⊥BD,
∴DF=BF,∠DOF=∠BOF.
∵四边形ABCD内接于⊙O,
∴∠A+∠C=180°.
∵∠C=2∠A,
∴∠A=60°,
∴∠BOD=120°,
∴∠BOF=60°.
∵OB=4,
∴BF=OB•sin∠BOF=4×sin60°=2$\sqrt{3}$,
∴BD=2BF=4$\sqrt{3}$.
故答案为:4$\sqrt{3}$.
点评 本题考查的是圆内接四边形的性质,熟知圆内接四边形的对角互补是解答此题的关键.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
12.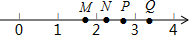 如图,M,N,P,Q是数轴上的四个点,这四个点钟最适合表示$\sqrt{7}$的是( )
如图,M,N,P,Q是数轴上的四个点,这四个点钟最适合表示$\sqrt{7}$的是( )
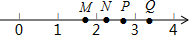 如图,M,N,P,Q是数轴上的四个点,这四个点钟最适合表示$\sqrt{7}$的是( )
如图,M,N,P,Q是数轴上的四个点,这四个点钟最适合表示$\sqrt{7}$的是( )| A. | M点 | B. | N点 | C. | P点 | D. | Q点 |
9.为进一步规范义务教育阶段的班额(每班学生数额),教育主管部门拟用两年的时间,将以前的班额从64降到50人.设平均每年降低的百分率为x,则关于x的方程为( )
| A. | 64(x+1)2=50 | B. | 50(x+1)2=64 | C. | 64(1-x)2=50 | D. | 50(1-x)2=64 |
16.已知点A(1,y1),B(2,y2),C(-3,y3)都在反比例函数y=$\frac{{{k^2}+1}}{x}$的图象上,则y1,y2,y3的大小关系是( )
| A. | y3<y1<y2 | B. | y1<y2<y3 | C. | y2<y1<y3 | D. | y3<y2<y1 |
6.近几年,随着电子商务的快速发展,“电商包裹件”占“快递件”总量的比例逐年增长,根据企业财报,某网站得到如下统计表:
(1)请选择适当的统计图,描述2014-2017年“电商包裹件”占当年“快递件”总量的百分比(精确到1%);
(2)若2018年“快递件”总量将达到675亿件,请估计其中“电商包裹件”约为多少亿件?
| 年份 | 2014 | 2015 | 2016 | 2017(预计) |
| 快递件总量(亿件) | 140 | 207 | 310 | 450 |
| 电商包裹件(亿件) | 98 | 153 | 235 | 351 |
(2)若2018年“快递件”总量将达到675亿件,请估计其中“电商包裹件”约为多少亿件?
13.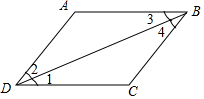 如图,若∠A+∠ABC=180°,则下列结论正确的是( )
如图,若∠A+∠ABC=180°,则下列结论正确的是( )
 如图,若∠A+∠ABC=180°,则下列结论正确的是( )
如图,若∠A+∠ABC=180°,则下列结论正确的是( )| A. | ∠1=∠2 | B. | ∠2=∠3 | C. | ∠1=∠3 | D. | ∠2=∠4 |
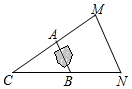 如图,A,B两点被池塘隔开,不能直接测量其距离.于是,小明在岸边选一点C,连接CA,CB,分别延长到点M,N,使AM=AC,BN=BC,测得MN=200m,则A,B间的距离为100m.
如图,A,B两点被池塘隔开,不能直接测量其距离.于是,小明在岸边选一点C,连接CA,CB,分别延长到点M,N,使AM=AC,BN=BC,测得MN=200m,则A,B间的距离为100m.