题目内容
9．为进一步规范义务教育阶段的班额（每班学生数额），教育主管部门拟用两年的时间，将以前的班额从64降到50人．设平均每年降低的百分率为x，则关于x的方程为（ ）| A． | 64（x+1）2=50 | B． | 50（x+1）2=64 | C． | 64（1-x）2=50 | D． | 50（1-x）2=64 |
分析 等量关系为：两年前的班额×（1-降低的百分比）×（1-降低的百分比）=现在的班额，把相关数量代入即可求得所求方程．
解答 解：设平均每年降低的百分率为x，根据题意得
64（1-x）2=50．
故选C．
点评 本题考查由实际问题抽象出一元二次方程．若设变化前的量为a，变化后的量为b，平均变化率为x，则经过两次变化后的数量关系为a（1±x）2=b．
练习册系列答案
相关题目
19．
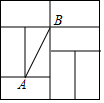如图是由8个全等的矩形组成的大正方形，线段AB的端点都在小矩形的顶点上，如果点P是某个小矩形的顶点，连接PA、PB，那么使△ABP为等腰直角三角形的点P的个数是（ ）
如图是由8个全等的矩形组成的大正方形，线段AB的端点都在小矩形的顶点上，如果点P是某个小矩形的顶点，连接PA、PB，那么使△ABP为等腰直角三角形的点P的个数是（ ）| A． | 2个 | B． | 3个 | C． | 4个 | D． | 5个 |
4．下列计算正确的是（ ）
| A． | 4a2-2a2=2 | B． | （a2）3=a5 | C． | a3•a6=a9 | D． | （2a2）3=6a6 |
14．能说明“对于任何实数a，|a|＞-a”是假命题的一个反例可以是（ ）
| A． | a=-2-1 | B． | a=$\frac{1}{3}$ | C． | a=1-3 | D． | a=π |
如图，已知四边形ABCD内接于半径为4的⊙O中，且∠C=2∠A，则BD=4$\sqrt{3}$．