题目内容
12．
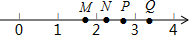如图，M，N，P，Q是数轴上的四个点，这四个点钟最适合表示$\sqrt{7}$的是（ ）| A． | M点 | B． | N点 | C． | P点 | D． | Q点 |
分析 直接估计得出$\sqrt{7}$的取值范围，进而得出答案．
解答 解：∵2＜$\sqrt{7}$＜3，
且2.52=6.25，
∴2.5＜$\sqrt{7}$＜3，
∴四个点钟最适合表示$\sqrt{7}$的是P点．
故选：C．
点评 此题主要考查了估算无理数的大小，正确得出$\sqrt{7}$的取值范围是解题关键．
练习册系列答案
相关题目
2．
如图所示的立方体，如果把它展开，可以是下列图形中的（ ）
如图所示的立方体，如果把它展开，可以是下列图形中的（ ）| A． |  | B． |  | C． |  | D． |  |
3．如图，从边长为a的大正方形中剪掉一个边长为b的小正方形，将阴影部分沿虚线剪开，拼成右边的矩形．根据图形的变化过程写出的一个正确的等式是（ ）
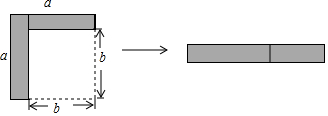
| A． | （a-b）2=a2-2ab+b2 | B． | a（a-b）=a2-ab | C． | （a-b）2=a2-b2 | D． | a2-b2=（a+b）（a-b） |
7．甲，乙两班进行跳绳比赛，参赛学生每分跳绳的个数统计结果如下表：
某同学分析上表后得出如下结论：
①甲、乙两班学生的平均成绩相同；
②乙班优秀的人数多于甲班优秀的人数（每分钟跳绳的个数≥150为优秀）；
③甲班成绩的波动比乙班大．上述结论中正确的是（ ）
| 班级 | 参赛人数 | 中位数 | 方差 | 平均字数 |
| 甲 | 55 | 149 | 191 | 135 |
| 乙 | 55 | 151 | 110 | 135 |
①甲、乙两班学生的平均成绩相同；
②乙班优秀的人数多于甲班优秀的人数（每分钟跳绳的个数≥150为优秀）；
③甲班成绩的波动比乙班大．上述结论中正确的是（ ）
| A． | ①②③ | B． | ①② | C． | ①③ | D． | ②③ |
4．下列计算正确的是（ ）
| A． | 4a2-2a2=2 | B． | （a2）3=a5 | C． | a3•a6=a9 | D． | （2a2）3=6a6 |
如图，已知四边形ABCD内接于半径为4的⊙O中，且∠C=2∠A，则BD=4$\sqrt{3}$．