题目内容
12.先化简,再求值:$\frac{{a}^{2}-3a}{{a}^{2}-1}$-$\frac{1}{1-a}$,其中a=$\sqrt{2}$-1.分析 先进行通分得到原式=$\frac{{a}^{2}-3a}{(a+1)(a-1)}$+$\frac{a+1}{(a-1)(a+1)}$,再进行同分母的加法运算,然后把分子分解因式后约分得到原式=$\frac{a-1}{a+1}$,再把a的值代入计算即可.
解答 解:原式=$\frac{{a}^{2}-3a}{(a+1)(a-1)}$+$\frac{a+1}{(a-1)(a+1)}$
=$\frac{{a}^{2}-3a+a+1}{(a+1)(a-1)}$
=$\frac{(a-1)^{2}}{(a+1)(a-1)}$
=$\frac{a-1}{a+1}$,
当a=$\sqrt{2}$-1时,原式=$\frac{\sqrt{2}-1-1}{\sqrt{2}-1+1}$=1-$\sqrt{2}$.
点评 本题考查了分式的化简求值:先把分式化简后,再把分式中未知数对应的值代入求出分式的值.在化简的过程中要注意运算顺序和分式的化简.化简的最后结果分子、分母要进行约分,注意运算的结果要化成最简分式或整式.

练习册系列答案
 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
2. 如图,已知直线AB∥CD,∠DCE=70°,∠A=30°则∠E的度数是( )
如图,已知直线AB∥CD,∠DCE=70°,∠A=30°则∠E的度数是( )
 如图,已知直线AB∥CD,∠DCE=70°,∠A=30°则∠E的度数是( )
如图,已知直线AB∥CD,∠DCE=70°,∠A=30°则∠E的度数是( )| A. | 30° | B. | 40° | C. | 50° | D. | 70° |
 如图,在直线AD上放置一个等腰直角三角形AOB和一个正方形BODC,∠AOB=90°,等腰直角三角形的直角边和正方形的边长均为2,⊙O1为正方形BODC的外接圆,动点P从点A出发以每秒$\sqrt{2}$个单位长度的速度沿A→B→A运动后停止;动点Q从点A出发以每秒2个单位长度的速度沿A→O→D→C→B运动,AO1交BO于E点,P、Q运动的时间为t(秒).
如图,在直线AD上放置一个等腰直角三角形AOB和一个正方形BODC,∠AOB=90°,等腰直角三角形的直角边和正方形的边长均为2,⊙O1为正方形BODC的外接圆,动点P从点A出发以每秒$\sqrt{2}$个单位长度的速度沿A→B→A运动后停止;动点Q从点A出发以每秒2个单位长度的速度沿A→O→D→C→B运动,AO1交BO于E点,P、Q运动的时间为t(秒). 如图AB是⊙O的直径,AC、DC为弦,∠ACD=60°,P为AB延长线上的点,∠APD=30°.
如图AB是⊙O的直径,AC、DC为弦,∠ACD=60°,P为AB延长线上的点,∠APD=30°.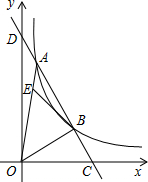 如图,一次函数与反比例函数y=$\frac{k}{x}$(x>0)的图象在第一象限交于A、B两点,交x轴于点C,交y轴于点D,且$\frac{CB}{BA}$=$\frac{1}{2}$,点E在线段OA上一点,OE=3EA,若△AEB的面积为1,则k的值是3.
如图,一次函数与反比例函数y=$\frac{k}{x}$(x>0)的图象在第一象限交于A、B两点,交x轴于点C,交y轴于点D,且$\frac{CB}{BA}$=$\frac{1}{2}$,点E在线段OA上一点,OE=3EA,若△AEB的面积为1,则k的值是3. 如图,已知AB∥CD∥EF,AD:AF=3:5,BE=12,那么CE的长等于$\frac{24}{5}$.
如图,已知AB∥CD∥EF,AD:AF=3:5,BE=12,那么CE的长等于$\frac{24}{5}$.