题目内容
20. 如图AB是⊙O的直径,AC、DC为弦,∠ACD=60°,P为AB延长线上的点,∠APD=30°.
如图AB是⊙O的直径,AC、DC为弦,∠ACD=60°,P为AB延长线上的点,∠APD=30°.(1)求证:DP是⊙O的切线;
(2)若⊙O的半径为5cm,求图中阴影部分的面积.
分析 (1)连接OD,求出∠AOD,求出∠DOB,求出∠ODP,根据切线判定推出即可;
(2)求出OP、DP长,分别求出扇形DOB和三角形ODP面积,即可求出答案.
解答 (1)证明: 连接OD,
连接OD,
∵∠ACD=60°,
∴由圆周角定理得:∠AOD=2∠ACD=120°,
∴∠DOP=180°-120°=60°,
∵∠APD=30°,
∴∠ODP=180°-30°-60°=90°,
∴OD⊥DP,
∵OD为半径,
∴DP是⊙O切线;
(2)解:∵∠P=30°,∠ODP=90°,OD=5cm,
∴OP=10cm,由勾股定理得:DP=5$\sqrt{3}$cm,
∴图中阴影部分的面积S=S△ODP-S扇形DOB=$\frac{1}{2}$×5×5$\sqrt{3}$-$\frac{60π×{5}^{2}}{360}$=($\frac{25\sqrt{3}}{2}$-$\frac{25}{6}$π)cm2.
点评 本题考查了扇形面积,三角形面积,切线的判定,圆周角定理等知识点的应用,主要考查学生的推理和计算能力.

练习册系列答案
相关题目
11.若一个三角形的三条边长分别为3,2a-1,6,则整数a的值可能是( )
| A. | 2,3 | B. | 3,4 | C. | 2,3,4 | D. | 3,4,5 |
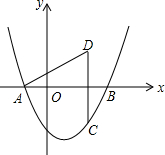 如图,抛物线为y=$\frac{\sqrt{3}}{3}$(x+1)(x-3)x轴交于A、B两点(点A在点B左侧),
如图,抛物线为y=$\frac{\sqrt{3}}{3}$(x+1)(x-3)x轴交于A、B两点(点A在点B左侧), 如图,在平行四边形ABCD中,点E,F分别为边BC,AD的中点.求证:四边形AECF是平行四边形.
如图,在平行四边形ABCD中,点E,F分别为边BC,AD的中点.求证:四边形AECF是平行四边形. 如图,已知一次函数的图象y=kx+b与反比例函数y=-$\frac{8}{x}$的图象交于A,B两点,且点A的横坐标和点B的纵坐标都是-2,求:
如图,已知一次函数的图象y=kx+b与反比例函数y=-$\frac{8}{x}$的图象交于A,B两点,且点A的横坐标和点B的纵坐标都是-2,求: