题目内容
17. 如图,已知AB∥CD∥EF,AD:AF=3:5,BE=12,那么CE的长等于$\frac{24}{5}$.
如图,已知AB∥CD∥EF,AD:AF=3:5,BE=12,那么CE的长等于$\frac{24}{5}$.
分析 根据平行线分线段成比例得到$\frac{AD}{AF}$=$\frac{BC}{BE}$,即$\frac{3}{5}$=$\frac{BC}{12}$,可计算出BC,然后利用CE=BE-BC进行计算.
解答 解:∵AB∥CD∥EF,
∴$\frac{AD}{AF}$=$\frac{BC}{BE}$,即$\frac{3}{5}$=$\frac{BC}{12}$,
∴BC=$\frac{36}{5}$,
∴CE=BE-BC=12-$\frac{36}{5}$=$\frac{24}{5}$.
故答案为:$\frac{24}{5}$.
点评 本题考查了平行线分线段成比例:三条平行线截两条直线,所得的对应线段成比例.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
7.十边形的内角和为( )
| A. | 360° | B. | 1440° | C. | 1800° | D. | 2160° |
7.下列各数中比0小的数是( )
| A. | -2 | B. | 1$\frac{1}{3}$ | C. | 3 | D. | $\sqrt{3}$ |
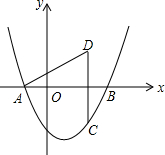 如图,抛物线为y=$\frac{\sqrt{3}}{3}$(x+1)(x-3)x轴交于A、B两点(点A在点B左侧),
如图,抛物线为y=$\frac{\sqrt{3}}{3}$(x+1)(x-3)x轴交于A、B两点(点A在点B左侧),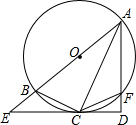 如图,已知AB为⊙O的直径,F为⊙O上一点,AC平分∠BAF且交⊙O于点C,过点C作CD⊥AF于点D,延长AB、DC交于点E,连接BC、CF.
如图,已知AB为⊙O的直径,F为⊙O上一点,AC平分∠BAF且交⊙O于点C,过点C作CD⊥AF于点D,延长AB、DC交于点E,连接BC、CF. 如图,已知一次函数的图象y=kx+b与反比例函数y=-$\frac{8}{x}$的图象交于A,B两点,且点A的横坐标和点B的纵坐标都是-2,求:
如图,已知一次函数的图象y=kx+b与反比例函数y=-$\frac{8}{x}$的图象交于A,B两点,且点A的横坐标和点B的纵坐标都是-2,求: 如图,半径为1的⊙P在射线AB上运动,且A(-3,0)B(0,3),那么当⊙P与坐标轴相切时,圆心P的坐标是(-2,1)或(-1,2)或(1,4).
如图,半径为1的⊙P在射线AB上运动,且A(-3,0)B(0,3),那么当⊙P与坐标轴相切时,圆心P的坐标是(-2,1)或(-1,2)或(1,4).