题目内容
1.计算:20160+|1-$\sqrt{2}$|-2cos45°+$\sqrt{8}$+(-$\frac{1}{3}$)-2.分析 根据实数的运算顺序,首先计算乘方、开方和乘法,然后从左向右依次计算,求出算式20160+|1-$\sqrt{2}$|-2cos45°+$\sqrt{8}$+(-$\frac{1}{3}$)-2的值是多少即可.
解答 解:20160+|1-$\sqrt{2}$|-2cos45°+$\sqrt{8}$+(-$\frac{1}{3}$)-2
=1+$\sqrt{2}$-1-2×$\frac{\sqrt{2}}{2}$+2$\sqrt{2}$+9
=$\sqrt{2}$-$\sqrt{2}$+2$\sqrt{2}$+9
=2$\sqrt{2}$+9
点评 (1)此题主要考查了实数的运算,要熟练掌握,解答此题的关键是要明确:在进行实数运算时,和有理数运算一样,要从高级到低级,即先算乘方、开方,再算乘除,最后算加减,有括号的要先算括号里面的,同级运算要按照从左到有的顺序进行.另外,有理数的运算律在实数范围内仍然适用.
(2)此题还考查了零指数幂的运算,要熟练掌握,解答此题的关键是要明确:①a0=1(a≠0);②00≠1.
(3)此题还考查了特殊角的三角函数值,要牢记30°、45°、60°角的各种三角函数值.
(4)此题还考查了负整数指数幂的运算,要熟练掌握,解答此题的关键是要明确:①a-p=$\frac{1}{{a}^{p}}$(a≠0,p为正整数);②计算负整数指数幂时,一定要根据负整数指数幂的意义计算;③当底数是分数时,只要把分子、分母颠倒,负指数就可变为正指数.

练习册系列答案
相关题目
11.若一个三角形的三条边长分别为3,2a-1,6,则整数a的值可能是( )
| A. | 2,3 | B. | 3,4 | C. | 2,3,4 | D. | 3,4,5 |
16.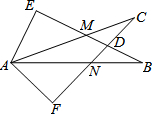 如图所示,∠E=∠F=90°,∠B=∠C,AE=AF,有以下结论:
如图所示,∠E=∠F=90°,∠B=∠C,AE=AF,有以下结论:
①EM=FN;②CD=DN;③∠FAN=∠EAM;④△ACN≌△ABM.
其中正确结论的个数为( )
 如图所示,∠E=∠F=90°,∠B=∠C,AE=AF,有以下结论:
如图所示,∠E=∠F=90°,∠B=∠C,AE=AF,有以下结论:①EM=FN;②CD=DN;③∠FAN=∠EAM;④△ACN≌△ABM.
其中正确结论的个数为( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
11.计算$\frac{2x}{{x}^{2}-1}$-$\frac{1}{x-1}$的结果是( )
| A. | x-1 | B. | $\frac{1}{x+1}$ | C. | $\frac{2}{x+1}$ | D. | 2x+1 |
 如图,已知一次函数的图象y=kx+b与反比例函数y=-$\frac{8}{x}$的图象交于A,B两点,且点A的横坐标和点B的纵坐标都是-2,求:
如图,已知一次函数的图象y=kx+b与反比例函数y=-$\frac{8}{x}$的图象交于A,B两点,且点A的横坐标和点B的纵坐标都是-2,求: 如图,半径为1的⊙P在射线AB上运动,且A(-3,0)B(0,3),那么当⊙P与坐标轴相切时,圆心P的坐标是(-2,1)或(-1,2)或(1,4).
如图,半径为1的⊙P在射线AB上运动,且A(-3,0)B(0,3),那么当⊙P与坐标轴相切时,圆心P的坐标是(-2,1)或(-1,2)或(1,4).