题目内容
19.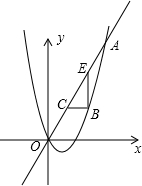 如图,已知抛物线y=$\frac{1}{2}$x2+bx与直线y=2x交于点O(0,0),A(a,16),点B是抛物线上O,A之间的一个动点,过点B分别作x轴、y轴的平行线与直线OA交于点C,E.
如图,已知抛物线y=$\frac{1}{2}$x2+bx与直线y=2x交于点O(0,0),A(a,16),点B是抛物线上O,A之间的一个动点,过点B分别作x轴、y轴的平行线与直线OA交于点C,E.(1)求抛物线的函数解析式;
(2)若OC=$\frac{3}{5}$AC,求BC的长;
(3)以BC,BE为边构造矩形BCDE,设点D的坐标为(m,n),直接写出m,n之间的关系式.
分析 (1)将点A的坐标代入直线解析式求出a的值,继而将点A的坐标代入抛物线解析式可得出b的值,继而得出抛物线解析式;
(2)根据OC=$\frac{3}{5}$AC以及点A的坐标,求出点C的坐标,将点B的纵坐标代入二次函数解析式求出点B的横坐标,继而可求出BC的长度;
(3)根据点D的坐标,可得出点E的坐标,点C的坐标,继而确定点B的坐标,将点B的坐标代入抛物线解析式可求出m,n之间的关系式.
解答 解:(1)∵点A(a,16)在直线y=2x上,
∴16=2a,
解得:a=8,
∴A(8,16).
又∵点A是抛物线y=$\frac{1}{2}$x2+bx上的一点,
∴16=$\frac{1}{2}$×82+8b,
解得b=-2,
∴抛物线解析式为y=$\frac{1}{2}$x2-2x;
(2)∵OC=$\frac{3}{5}$AC,A(8,16),
∴C(3,6),
∴点B的纵坐标是6,
∴$\frac{1}{2}$x2-2x=6,解得x1=6,x2=-2,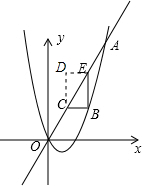 ∴点B的坐标是(6,6),
∴点B的坐标是(6,6),
∴BC=6-3=3;
(3)∵直线OA的解析式为:y=2x,
点D的坐标为(m,n),
∴点E的坐标为($\frac{1}{2}$n,n),点C的坐标为(m,2m),
∴点B的坐标为($\frac{1}{2}$n,2m),
把点B($\frac{1}{2}$n,2m)代入y=$\frac{1}{2}$x2-2x,可得2m=$\frac{1}{2}$•($\frac{1}{2}$n)2-2×$\frac{1}{2}$n,
∴m、n之间的关系式为m=$\frac{1}{16}$n2-$\frac{1}{2}$n.
点评 本题是二次函数综合题,其中涉及到利用待定系数法求二次函数的解析式,函数图象上点的坐标特征,两点间的距离公式,矩形的性质等知识,解答本题需要同学们能理解矩形四个顶点的坐标之间的关系.

| A. | “任意画出一个圆,它是中心对称图形”是随机事件 | |
| B. | 为了解我省中学生的体能情况,应采用普查的方式 | |
| C. | 天气预报明天下雨的概率是99%,说明明天一定会下雨 | |
| D. | 任意掷一枚质地均匀的硬币10次,正面朝上的次数不一定是5次 |
| A. | 相等的圆周角所对的弧相等 | |
| B. | 方程x2-x+1=0有两个不等实根 | |
| C. | 同一个角的正弦值和余弦值的和等于1 | |
| D. | 圆的切线垂直于过切点的半径 |
 如图,在?ABCD中,对角线AC、BD相交于点O,点E、F分别是AD、CD的中点,则△OEF的面积S1与△BOC面积S2的关系是( )
如图,在?ABCD中,对角线AC、BD相交于点O,点E、F分别是AD、CD的中点,则△OEF的面积S1与△BOC面积S2的关系是( )| A. | S1=S2 | B. | S1>S2 | C. | S1<S2 | D. | $S1=\frac{1}{2}S2$ |
| A | B | C | D | |
| 2月份售价(元/盒) | 15.4 | 8.6 | 11.2 | 28.2 |
| 3月份售价(元/盒) | 12.8 | 7.7 | 10 | 20.5 |
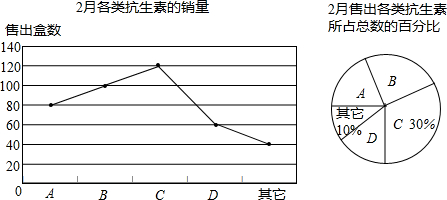
(2)补全扇形统计图;
(3)吴老师到该药房买一些抗生素作为家里备用药,在A、B、C、D各一盒中随机购买两盒,请用画树状图或列表法求出他刚好选中A和B的概率.