题目内容
14．为喜迎新年，九三班上学期期末开展了“元旦游园”活动．其中一项是抽奖获奖品的活动：抽奖箱中有4个标号分别为1，2，3，4的质地、大小完全相同的小球．参与的同学任意摸取一个小球，然后放回，搅匀后再摸取一个小球．若两次摸出的数字之和是“8”为一等奖，可获签字笔一支；数字之和是“6”为二等奖，可获铅笔一支；数字之和其他数字则为三等奖，可获橡皮擦一个．（1）参与抽奖的获三等奖的概率为$\frac{3}{4}$；
（2）分别求出参与抽奖获一等奖和二等奖的概率．
分析 （1）根据题意可以写出所有的可能性以及所有的可能性之和，从而可以求得参与抽奖的获三等奖的概率；
（2）根据第（1）问中写出数据可以得到参与抽奖获一等奖和二等奖的概率．
解答 解：（1）由题意可得，抽取两次所有的可能性为：
（1，1）、（1，2）、（1，3）、（1，4）、
（2，1）、（2，2）、（2，3）、（2，4）、
（3，1）、（3，2）、（3，3）、（3，4）、
（4，1）、（4，2）、（4，3）、（4，4），
抽取两次所有可能性的和为：
2、3、4、5、
3、4、5、6、
4、5、6、7、
5、6、7、8，
∴参与抽奖的获三等奖的概率为：$\frac{12}{16}$=$\frac{3}{4}$，
故答案为：$\frac{3}{4}$；
（2）由（1）列出所有可能性以及所有可能性之和可得，
参与抽奖获一等奖的概率为：$\frac{1}{16}$，
参与抽奖获二等奖的概率为：$\frac{3}{16}$．
点评 本题考查列表法与树状图法，解题的关键是明确题意，写出所有的可能性以及所有可能性之和．
练习册系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
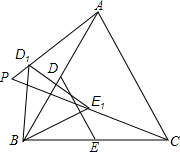已知：在等边△ABC中，AB=2$\sqrt{3}$，D、E分别是AB，BC的中点（如图），若将△BDE绕点B逆时针旋转，得到△BD1E1．设旋转的角为α（0°＜α＜180°），记射线CE1与AD1的交点为P，点P到BC所在直线的距离的最大值为2．
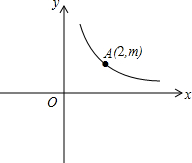在平面直角坐标系xOy中，反比例函数y=$\frac{k}{x}$（k＞0）的图象经过点A（2，m），连接OA，在x轴上有一点B，且AO=AB，△AOB的面积为2．
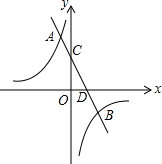如图，在平面直角坐标系xOy中，一次函数y=k1x+b与反比例函数y=$\frac{{k}_{2}}{x}$的图象交于点A（-1，6）和点B（3，m），与y轴交于点C，与x轴交于点D．
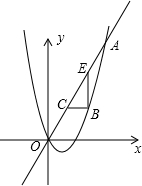如图，已知抛物线y=$\frac{1}{2}$x2+bx与直线y=2x交于点O（0，0），A（a，16），点B是抛物线上O，A之间的一个动点，过点B分别作x轴、y轴的平行线与直线OA交于点C，E．
6．有三张背面完全相同、正面分别写有整数-1，1，2的卡片，现将这三张卡片背面朝上洗匀随机抽取一张，正面的数记为m，再从剩余的两张卡片中随机抽取一张，其正面上的数记为n，则m•n的值是负数的概率为（ ）
| A． | $\frac{1}{6}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{2}$ | D． | $\frac{2}{3}$ |