题目内容
已知一个二次函数的图象过点A(-1,10),B(1,4),C(2,7),点D和点B关于抛物线的对称轴对称,问是否存在与抛物线只有一个公共点D的直线?如果存在,求出符合条件的直线;如果不存在,请说明理由.
考点:待定系数法求二次函数解析式,根的判别式,二次函数的性质
专题:计算题
分析:存在,设抛物线解析式为y=ax2+bx+c,把A,B,C代入求出a,b,c的值,确定出抛物线解析式,得出对称轴,由D与B关于对称轴对称求出D坐标,代入表示出m,进而求出过D的解析式,联立后消去y得到关于x的一元二次方程,令根的判别式等于0求出k的值,即可得出满足题意的解析式.
解答:解:存在,设抛物线解析式为y=ax2+bx+c,
把A、B、C坐标代入得:
,
解得:
,
∴抛物线解析式为y=2x2-3x+5,对称轴为直线x=
,
∵点D与B关于对称轴对称,
∴D(
,4),
设过点D的直线为y=kx+m,把D坐标代入得:
k+m=4,即m=4-
k,
∴过D的解析式为y=kx+4-
k,
联立y=2x2-3x+5得:2x2-3x+5=kx+4-
k,
整理得:2x2-(3+k)x+
k+1=0,
令△=0,得:(3+k)2-8(
k+1)=0,
解得:k=-1,
则符合题意的解析式为y=-x+
.
把A、B、C坐标代入得:
|
解得:
|
∴抛物线解析式为y=2x2-3x+5,对称轴为直线x=
| 3 |
| 4 |
∵点D与B关于对称轴对称,
∴D(
| 1 |
| 2 |
设过点D的直线为y=kx+m,把D坐标代入得:
| 1 |
| 2 |
| 1 |
| 2 |
∴过D的解析式为y=kx+4-
| 1 |
| 2 |
联立y=2x2-3x+5得:2x2-3x+5=kx+4-
| 1 |
| 2 |
整理得:2x2-(3+k)x+
| 1 |
| 2 |
令△=0,得:(3+k)2-8(
| 1 |
| 2 |
解得:k=-1,
则符合题意的解析式为y=-x+
| 9 |
| 2 |
点评:此题考查了待定系数法求二次函数解析式,熟练掌握待定系数法是解本题的关键.

练习册系列答案
相关题目
“从一个布袋中闭上眼睛随机摸出一球恰是黄球的概率为
”的意思是( )
| 1 |
| 5 |
| A、摸球5次就一定有1次摸出黄球 |
| B、摸球5次就一定有4次不能摸出黄球 |
| C、布袋中一定有一个黄球和4个别的颜色的球 |
| D、如果摸球次数很多,那么平均每摸球5次便有1次摸出黄球 |
分式
中,x、y同时扩大为原来的2倍时,分式的值的变化为( )
| 2x-y |
| xy |
A、缩小为原值的
| ||
B、缩小为原值的
| ||
C、缩小为原值的
| ||
| D、不变 |
下列四句话中,错误的是( )
| A、存在最大的负整数 |
| B、不存在最小的有理数 |
| C、若|a|=-a,则a<0 |
| D、若|a|=a,则a≥0 |
 如图,小正方形的边长为1,试说明△ABC是等腰直角三角形.
如图,小正方形的边长为1,试说明△ABC是等腰直角三角形.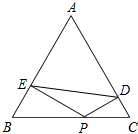 如图,已知P是等边△ABC的BC边上任意一点,过P点分别作AB、AC的垂线PE、PD,垂足为E、D.问:△AED的周长与四边形EBCD的周长之间的关系?
如图,已知P是等边△ABC的BC边上任意一点,过P点分别作AB、AC的垂线PE、PD,垂足为E、D.问:△AED的周长与四边形EBCD的周长之间的关系?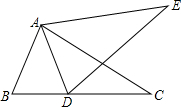 如图,D是BC上一点,AB=AD,BC=DE.△ABC≌△ADE,求证:∠CDE=∠BAD.
如图,D是BC上一点,AB=AD,BC=DE.△ABC≌△ADE,求证:∠CDE=∠BAD.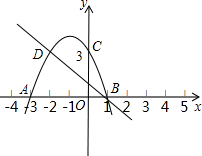 如图,二次函数的图象与x轴交于A、B两点,与y轴交于点C,点C、D是二次函数图象上的一对对称点,一次函数的图象过点B、D.
如图,二次函数的图象与x轴交于A、B两点,与y轴交于点C,点C、D是二次函数图象上的一对对称点,一次函数的图象过点B、D.