题目内容
11.△ABC中,∠C=90°,CD⊥AB于点D,若AD=8,BC=12,则AB=4+4$\sqrt{10}$.分析 先证明△BCD∽△BAC,得$\frac{BC}{BA}$=$\frac{BD}{BC}$,设BD=x,可得方程$\frac{12}{x+8}$=$\frac{x}{12}$,求出x即可解决问题.
解答 解:如图,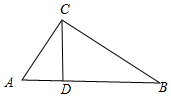
∵CD⊥AB,
∴∠BDC=∠ACB=90°,∵∠B=∠B,
∴△BCD∽△BAC,
∴$\frac{BC}{BA}$=$\frac{BD}{BC}$,
设BD=x,
∴$\frac{12}{x+8}$=$\frac{x}{12}$,
解得x=4$\sqrt{10}$-4或-4$\sqrt{10}$-4(舍弃),
∴AB=AD+BD=8+4$\sqrt{10}$-4=4+4$\sqrt{10}$,
故答案为4+4$\sqrt{10}$.
点评 本题考查相似三角形的判定和性质,解题的关键是熟练掌握相似三角形的判定和性质,学会用方程的思想思考问题,属于中考常考题型.

练习册系列答案
相关题目
6.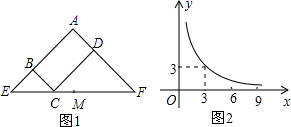 图1所示矩形ABCD中,BC=x,CD=y,y与x满足的反比例函数关系如图2所示,等腰直角三角形AEF的斜边EF过点C,M为EF的中点,则下列结论正确的是( )
图1所示矩形ABCD中,BC=x,CD=y,y与x满足的反比例函数关系如图2所示,等腰直角三角形AEF的斜边EF过点C,M为EF的中点,则下列结论正确的是( )
 图1所示矩形ABCD中,BC=x,CD=y,y与x满足的反比例函数关系如图2所示,等腰直角三角形AEF的斜边EF过点C,M为EF的中点,则下列结论正确的是( )
图1所示矩形ABCD中,BC=x,CD=y,y与x满足的反比例函数关系如图2所示,等腰直角三角形AEF的斜边EF过点C,M为EF的中点,则下列结论正确的是( )| A. | 当x=3时,EC<EM | B. | 当x=9时,EC<EM | ||
| C. | 当x增大时,BE•DF的值不变 | D. | 当x增大时,EC•CF的值增大 |
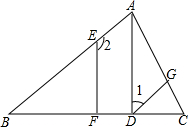 如图:已知AD⊥BC于点D,∠1+∠2=180°,∠B=∠CDG,试判断EF与BC的位置关系并说明理由.
如图:已知AD⊥BC于点D,∠1+∠2=180°,∠B=∠CDG,试判断EF与BC的位置关系并说明理由.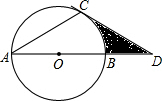 如图,⊙O的直径AB为12点D在AB的延长线上,DC切⊙O于点C,且∠DAC=30°,则图中阴影部分面积为18$\sqrt{3}$-6π.
如图,⊙O的直径AB为12点D在AB的延长线上,DC切⊙O于点C,且∠DAC=30°,则图中阴影部分面积为18$\sqrt{3}$-6π.