题目内容
20.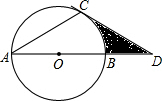 如图,⊙O的直径AB为12点D在AB的延长线上,DC切⊙O于点C,且∠DAC=30°,则图中阴影部分面积为18$\sqrt{3}$-6π.
如图,⊙O的直径AB为12点D在AB的延长线上,DC切⊙O于点C,且∠DAC=30°,则图中阴影部分面积为18$\sqrt{3}$-6π.
分析 连接OC,由圆周角定理得出∠BOC=2∠DAC=60°,可求得∠D=30°,得出OD=2OC=12,由勾股定理求出CD,利用△OCD的面积-扇形BOC的面积求得阴影部分的面积.
解答 解:连接OC,如图所示: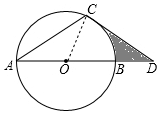
∵DC切⊙O于点C,
∴DC⊥OC,
∵∠BOC=2∠DAC=60°,
∴∠D=30°,
在Rt△OCD中,OC=$\frac{1}{2}$AB=6,
∴OD=2OC=12,
由勾股定理得:CD=$\sqrt{3}$OC=6$\sqrt{3}$,
∴S△OCD=$\frac{1}{2}$OC•CD=$\frac{1}{2}$×6×6$\sqrt{3}$=18$\sqrt{3}$,
∵∠COD=60°,
∴S扇形COB=$\frac{60π×{6}^{2}}{360}$=6π,
∴S阴影=S△OCD-S扇形COB=18$\sqrt{3}$-6π;
故答案为:18$\sqrt{3}$-6π.
点评 本题主要考查切线的性质、圆周角定理、直角三角形的性质、勾股定理及扇形面积的计算;熟练掌握切线的性质,连接过切点的半径是解题的关键.

练习册系列答案
相关题目
10.如图,将左边正方形剪成四块,恰能拼成右边的矩形,若a=2,则b的值是( )
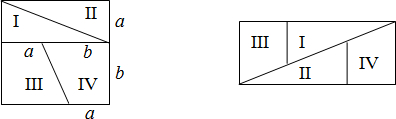

| A. | $\sqrt{5}$ | B. | $\sqrt{3}$ | C. | $\sqrt{5}$+1 | D. | $\sqrt{3}$+1 |
 如图,在△ABC中,AB=5,AC=3,AD、AE分别是它的角平分线和中线,过点C作CG⊥AD,垂足为点F,连接EF,则EF=1.
如图,在△ABC中,AB=5,AC=3,AD、AE分别是它的角平分线和中线,过点C作CG⊥AD,垂足为点F,连接EF,则EF=1.
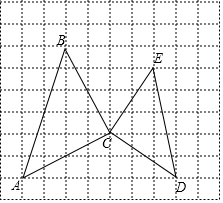 在如图10×9的网格图中,△ABC和△CDE都是等腰直角三角形,其顶点都在格点上,若点A、C的坐标分别为(-5,-2)和(-1,0).
在如图10×9的网格图中,△ABC和△CDE都是等腰直角三角形,其顶点都在格点上,若点A、C的坐标分别为(-5,-2)和(-1,0).