题目内容
11.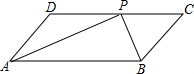 如图,在?ABCD中,∠ABC与∠BAD的平分线交于点P,且点P在CD边上.
如图,在?ABCD中,∠ABC与∠BAD的平分线交于点P,且点P在CD边上.(1)求∠APB的度数;
(2)若AD=10,AP=16,求△ABP的周长.
分析 (1)由平行四边形的性质得出AD∥BC,AD=BC,AB=CD,得出∠ABC+∠BAD=180°,由角平分线得出∠ABP=∠CBP=$\frac{1}{2}$∠ABC,∠BAP=$\frac{1}{2}$∠BAD,即可得出结果;
(2)证出∠BPC=∠CBP,得出PC=BC=AD=10,同理:PD=AD=10,因此AB=CD=20,由勾股定理求出BP,即可得出结果.
解答 解:(1)∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,AD=BC,AB=CD,
∴∠ABC+∠BAD=180°,
∵∠ABC与∠BAD的平分线交于点P,
∴∠ABP=∠CBP=$\frac{1}{2}$∠ABC,∠BAP=$\frac{1}{2}$∠BAD,
∴∠ABP+∠BAP=$\frac{1}{2}$×180°=90°;
(2)∵AB∥CD,
∴∠ABP=∠BPC,
∵∠ABP=∠CBP,
∴∠BPC=∠CBP,
∴PC=BC=AD=10,
同理:PD=AD=10,
∴AB=CD=20,
∵∠APB=90°,AP=16,
∴BP=$\sqrt{A{B}^{2}-A{P}^{2}}$=$\sqrt{2{0}^{2}-1{6}^{2}}$=12,
∴△ABP的周长=AB+AP+BP=20+16+12=48.
点评 此题主要考查了角平分线的定义、平行四边形的性质、平行线的性质、等腰三角形的判定、勾股定理等知识;熟练掌握平行四边形的性质,证明等腰三角形是解决问题(2)的关键.

练习册系列答案
相关题目
6.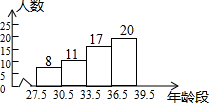 菲尔兹奖(Fields Medal)是享有崇高声誉的数学大奖,每四年颁奖一次,颁给二至四名成就显著的年轻数学家,下面是对截至2015年56名获奖者的年龄进行统计得到的统计图.则下列说法中正确的是( )
菲尔兹奖(Fields Medal)是享有崇高声誉的数学大奖,每四年颁奖一次,颁给二至四名成就显著的年轻数学家,下面是对截至2015年56名获奖者的年龄进行统计得到的统计图.则下列说法中正确的是( )
 菲尔兹奖(Fields Medal)是享有崇高声誉的数学大奖,每四年颁奖一次,颁给二至四名成就显著的年轻数学家,下面是对截至2015年56名获奖者的年龄进行统计得到的统计图.则下列说法中正确的是( )
菲尔兹奖(Fields Medal)是享有崇高声誉的数学大奖,每四年颁奖一次,颁给二至四名成就显著的年轻数学家,下面是对截至2015年56名获奖者的年龄进行统计得到的统计图.则下列说法中正确的是( )| A. | 平均年龄是37.5岁 | B. | 中位数年龄位于33.5-36.5岁 | ||
| C. | 众数年龄位于36.5-39.5岁 | D. | 以上选项都不正确 |
6. 如图所示,将含有30°角的三角板的直角顶点放在相互平行的两条直线其中一条上,若∠1=32°,则∠2的度数为( )
如图所示,将含有30°角的三角板的直角顶点放在相互平行的两条直线其中一条上,若∠1=32°,则∠2的度数为( )
 如图所示,将含有30°角的三角板的直角顶点放在相互平行的两条直线其中一条上,若∠1=32°,则∠2的度数为( )
如图所示,将含有30°角的三角板的直角顶点放在相互平行的两条直线其中一条上,若∠1=32°,则∠2的度数为( )| A. | 25° | B. | 28° | C. | 30° | D. | 32° |
20.若$\frac{1}{\sqrt{2x-1}}$在实数范围内有意义,则x的取值范围是( )
| A. | x>$\frac{1}{2}$ | B. | x≥$\frac{1}{2}$ | C. | x<$\frac{1}{2}$ | D. | x>0 |
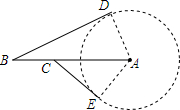 如图所示,某海域直径为30n mile的暗礁区中心有一哨所A,值班人员发现有一轮船从哨所的正西方向90n mile的B处向哨所驶来,哨所及时向轮船发出了危险信号,但轮船没有收到信号,又继续前进了15n mile到达C处,此时哨所第二次发出紧急信号.
如图所示,某海域直径为30n mile的暗礁区中心有一哨所A,值班人员发现有一轮船从哨所的正西方向90n mile的B处向哨所驶来,哨所及时向轮船发出了危险信号,但轮船没有收到信号,又继续前进了15n mile到达C处,此时哨所第二次发出紧急信号. 双休日,小明在公园放风筝,如图,拿风筝线的手A离地面高度AE为1.5米,风筝飞到C处时的线长AC为30米,这时测得∠CAB=60°
双休日,小明在公园放风筝,如图,拿风筝线的手A离地面高度AE为1.5米,风筝飞到C处时的线长AC为30米,这时测得∠CAB=60° 有理数a、b在数轴上的位置如图所示,那么a+b<0(填“>”、“<”或“=”)
有理数a、b在数轴上的位置如图所示,那么a+b<0(填“>”、“<”或“=”) 如图,已知AB∥CD,BC∥AD,问∠B与∠D有怎样的大小关系,为什么?
如图,已知AB∥CD,BC∥AD,问∠B与∠D有怎样的大小关系,为什么?