题目内容
15.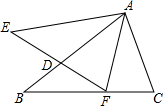 如图,△ABC与△AEF中,AB=AE,BC=EF,∠B=∠E,AB交EF于D.给出下列结论:
如图,△ABC与△AEF中,AB=AE,BC=EF,∠B=∠E,AB交EF于D.给出下列结论:①DF=CF;②∠AFC=∠C;③△ADE∽△FDB;④∠BFD=∠CAF.
其中正确的结论是②③④(填序号)
分析 先根据已知条件证明△AEF≌△ABC,从中找出对应角或对应边.然后根据角之间的关系找相似,即可解答.
解答 解:在△ABC与△AEF中$\left\{\begin{array}{l}{AB=AE}\\{∠B=∠E}\\{BC=EF}\end{array}\right.$,
∴△AEF≌△ABC,
∴AF=AC,
∴∠AFC=∠C;
由∠B=∠E,∠ADE=∠FDB,
可知:△ADE∽△FDB;
∵∠EAF=∠BAC,
∴∠EAD=∠CAF,
由△ADE∽△FD,B可得∠EAD=∠BFD,
∴∠BFD=∠CAF.
综上可知:②③④正确.
故答案为:②③④.
点评 本题主要考查了全等三角形的判定与性质,相似三角形的判定和性质,熟练掌握全等三角形的判定与性质是解决问题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
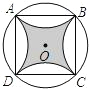 如图是圆内接正方形ABCD,分别将$\widehat{AB}$,$\widehat{BC}$,$\widehat{CD}$,$\widehat{DA}$,沿边长AB,BC,CD,DA向内翻折,已知BD=2,则阴影部分的面积为4-4π.
如图是圆内接正方形ABCD,分别将$\widehat{AB}$,$\widehat{BC}$,$\widehat{CD}$,$\widehat{DA}$,沿边长AB,BC,CD,DA向内翻折,已知BD=2,则阴影部分的面积为4-4π. 如图,在平行四边形ABCD中,BE平分∠ABC交AD于点E,DF平分∠ADE交BC于点F.若BD⊥EF,请判断四边形EBFD是什么四边形,并说明理由.
如图,在平行四边形ABCD中,BE平分∠ABC交AD于点E,DF平分∠ADE交BC于点F.若BD⊥EF,请判断四边形EBFD是什么四边形,并说明理由.
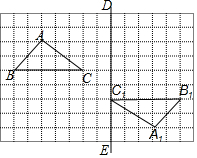 如图,在方格纸中,每个小正方形的边长都为1个单位长度,△ABC与△A1B1C1呈中心对称.
如图,在方格纸中,每个小正方形的边长都为1个单位长度,△ABC与△A1B1C1呈中心对称.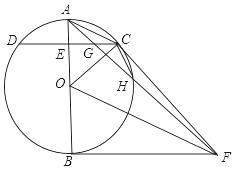 如图,已知AB是⊙O的直径,C是⊙O上任一点(不与A,B重合),AB⊥CD于E,BF为⊙O的切线,OF∥AC,连结AF,FC,AF与CD交于点G,与⊙O交于点H,连结CH.
如图,已知AB是⊙O的直径,C是⊙O上任一点(不与A,B重合),AB⊥CD于E,BF为⊙O的切线,OF∥AC,连结AF,FC,AF与CD交于点G,与⊙O交于点H,连结CH.