题目内容
已知在△ABC中,D为BC上一点,若
=
,则△ABD、△ADC、△ABC的面积关系为 .
| BD |
| DC |
| 2 |
| 3 |
考点:三角形的面积
专题:
分析:根据三角形的面积即是底边×对应的高,求得∴
=
=
,又S△ABC=S△ABD+S△ADC,继而即可求出答案.
| S△ABD |
| S△ADC |
| BD |
| DC |
| 2 |
| 3 |
解答:解∵△ABD和△ACD底边BD和CD所对应的高相等,设为h,
∴
=
=
=

∵S△ABC=S△ABD+S△ADC,
∴S△ABD:S△ADC:SABC=2:3:5
故答案为:2:3:5.
∴
| S△ABD |
| S△ADC |
| ||
|
| BD |
| DC |
| 2 |
| 3 |

∵S△ABC=S△ABD+S△ADC,
∴S△ABD:S△ADC:SABC=2:3:5
故答案为:2:3:5.
点评:本题考查了三角形的面积,难度不大,注意熟练掌握三角形的面积公式是关键.

练习册系列答案
相关题目
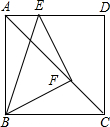 如图,已知正方形ABCD,在AD、AC上分别取E、F两点,使ED:AD=2FC:AC,求证:△BEF是等腰直角三角形.
如图,已知正方形ABCD,在AD、AC上分别取E、F两点,使ED:AD=2FC:AC,求证:△BEF是等腰直角三角形.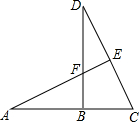 如图,已知BD⊥AC,AE⊥CD,BF=BC,求证:AF=CD.
如图,已知BD⊥AC,AE⊥CD,BF=BC,求证:AF=CD. 如图是某房间木地板的一个图案,其中AB=BC=CD=DA,AE=EC=CF=FA.图案由有花纹的全等三角形木块(阴影部分)与无花纹的全等三角形木块(中间部分)拼成,这个图案的面积是0.05m2.如果房间的面积是13m2,那么最少需要有花纹的三角形木块和无花纹的三角形木块各多少块?
如图是某房间木地板的一个图案,其中AB=BC=CD=DA,AE=EC=CF=FA.图案由有花纹的全等三角形木块(阴影部分)与无花纹的全等三角形木块(中间部分)拼成,这个图案的面积是0.05m2.如果房间的面积是13m2,那么最少需要有花纹的三角形木块和无花纹的三角形木块各多少块?