题目内容
8．已知|x-12|+（y-13）2+z2-10z+25=0，则以x，y，z为三边边长的三角形的形状是直角 三角形．分析 根据非负数的性质求出x、y、z的值，求出x2+z2=y2，根据勾股定理的逆定理判断即可．
解答 解：∵|x-12|+（y-13）2+z2-10z+25=0，
∴x-12=0，y-13=0，z-5=0，
∴x=12，y=13，z=5，
∴x2+z2=y2，
∴以x、y、z为三边的三角形是直角三角形，
故答案为：直角．
点评 本题考查了绝对值，偶次方，勾股定理的逆定理的应用，解此题的关键是求出x2+z2=y2．
练习册系列答案
相关题目
如图，在四边形ABCD中，∠A=∠B，CB=CE．求证：CE∥AD．
16．两个代数式x-1与x-3的值的符号相同，则x的取值范围是（ ）
| A． | x＞3 | B． | x＜1 | C． | 1＜x＜3 | D． | x＜1或x＞3 |
如图所示，△ABC平移到△A′B′C′的位置的过程是：将△ABC先向上平移1格，再向右平移3格后得到△A′B′C′．
17．
菲尔兹奖是国际上享有崇高声誉的一个数学奖项，每4年评选一次，颁给有卓越贡献的年轻数学家，被视为数学界的诺贝尔奖．下面的数据是从1936年至2014年45岁以下菲尔兹奖得住获奖时的年龄（岁）：
39 35 33 39 27 33 35 31 31 37 32 38 36 31 39 32 38 37
34 34 38 32 35 36 33 32 35 36 37 39 38 40 38 37 39 38
34 33 40 36 36 37 31 38 38 37 35 40 39 37
请根据以上数据，解答以下问题：
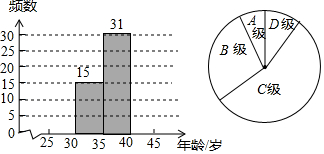
（1）小彬按“组距为5”列出了如下的频数分布表，每组数据含最小值不含最大值，请将表中空缺的部分补充完整，并补全频数分布直方图：
（2）在（1）的基础上，小彬又画出了如图所示的扇形统计图，图中B组所对的圆心角的度数为108°；
（3）根据（1）中的频数分布直方图试描述这50位菲尔兹奖得主获奖时的年龄的分布特征．
菲尔兹奖是国际上享有崇高声誉的一个数学奖项，每4年评选一次，颁给有卓越贡献的年轻数学家，被视为数学界的诺贝尔奖．下面的数据是从1936年至2014年45岁以下菲尔兹奖得住获奖时的年龄（岁）：39 35 33 39 27 33 35 31 31 37 32 38 36 31 39 32 38 37
34 34 38 32 35 36 33 32 35 36 37 39 38 40 38 37 39 38
34 33 40 36 36 37 31 38 38 37 35 40 39 37
请根据以上数据，解答以下问题：
（1）小彬按“组距为5”列出了如下的频数分布表，每组数据含最小值不含最大值，请将表中空缺的部分补充完整，并补全频数分布直方图：
| 分组 | 频数 |
| A：25～30 | 1 |
| B：30～35 | 15 |
| C：35～40 | 31 |
| D：40～45 | 3 |
| 总 计 | 50 |
（3）根据（1）中的频数分布直方图试描述这50位菲尔兹奖得主获奖时的年龄的分布特征．
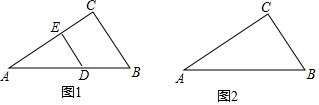
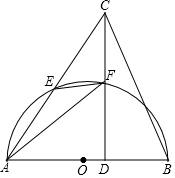如图，在△ABC中，CD⊥AB，垂足为点D．以AB为直径的半⊙O分别与