题目内容
5．
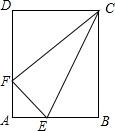如图，将矩形ABCD沿CE折叠，点B恰好落在边AD上的点F处，如果$\frac{AB}{BC}=\frac{3}{4}$，那么tan∠DCF=$\frac{\sqrt{7}}{3}$．
分析 设AB=3λ，则BC=4λ；首先证明CF=CB=4λ；运用勾股定理求出DF的长，即可解决问题．
解答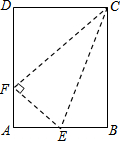 
解：如图，设AB=3λ，则BC=4λ；
∵四边形ABCD为矩形，
∴DC=AB=3λ，∠D=90°；
由题意得：CF=CB=4λ，
由勾股定理得：DF2=CF2-CD2，
解得：DF=$\sqrt{7}$λ，
∴tan∠DCF=$\frac{DF}{CD}$=$\frac{\sqrt{7}}{3}$，
故答案为$\frac{\sqrt{7}}{3}$．
点评 本题考查了翻折变换的性质、勾股定理，牢固掌握翻折变换的性质、勾股定理是基础，灵活运用是关键．
练习册系列答案
相关题目
王杰为了测量他家小楼附近楼房AB的高度，他从楼底的B处测得到他家小楼顶部D的仰角∠CBD为30°，又测得两幢楼之间的距离BC为10$\sqrt{3}$m．（以下计算结果精确到0.1m，参考值$\sqrt{2}$≈1.414，$\sqrt{3}$≈1.732，$\sqrt{5}$≈2.236）
如图，直线y=3x和y=kx+2相交于点P（a，3），则不等式3x≥kx+2的解集为x≥1．
10．
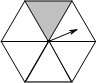如图，一个正六边形转盘被分成6个全等的正三角形．任意旋转这个转盘1次，当转盘停止转动时，指针指向阴影区域的概率是（ ）
如图，一个正六边形转盘被分成6个全等的正三角形．任意旋转这个转盘1次，当转盘停止转动时，指针指向阴影区域的概率是（ ）| A． | $\frac{1}{2}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{4}$ | D． | $\frac{1}{6}$ |
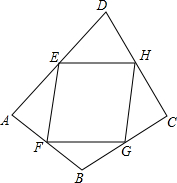如图，在四边形ABCD中，AD=CD=8，AB=CB=6，点E、F、G、H分别是DA、AB、BC、CD的中点．
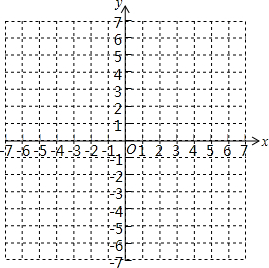在图中画出函数y=-x+1，y=2x-5的图象，利用图象回答下列问题：