题目内容
15.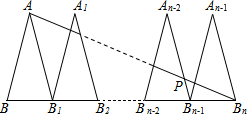 如图,△ABB1,△A1B1B2,…,△An-2Bn-2Bn-1,△An-1Bn-1Bn是n个全等的等腰三角形,其中AB=2,BB1=1,底边BB1,B1B2,…,Bn-2Bn-1,Bn-1Bn在同一条直线上,连接ABn交An-2Bn-1于点P,则PBn-1的值为$\frac{2}{n-1}$.
如图,△ABB1,△A1B1B2,…,△An-2Bn-2Bn-1,△An-1Bn-1Bn是n个全等的等腰三角形,其中AB=2,BB1=1,底边BB1,B1B2,…,Bn-2Bn-1,Bn-1Bn在同一条直线上,连接ABn交An-2Bn-1于点P,则PBn-1的值为$\frac{2}{n-1}$.
分析 根据全等三角形的性质得到∠AB1B=∠PBn-1B,根据平行线的判定得到AB1∥PBn-1,根据相似三角形的性质即可得到结论.
解答 解:∵△ABB1,△A1B1B2,…,△An-2Bn-2Bn-1,△An-1Bn-1Bn是n个全等的等腰三角形,
∴∠AB1B=∠PBn-1B,
∴AB1∥PBn-1,
∴PBnBn-1∽△ABnB1,
∴$\frac{P{B}_{n-1}}{A{B}_{1}}$=$\frac{{B}_{n}{B}_{n-1}}{{B}_{n}{B}_{1}}$,
∵AB1=AB=2,B1Bn=n-1,BnBn-1=1,
∴$\frac{P{B}_{n-1}}{2}$=$\frac{1}{n-1}$,
∴PBn-1=$\frac{2}{n-1}$.
故答案为:$\frac{2}{n-1}$.
点评 本题考查了相似三角形的判定和性质,全等三角形的性质,等腰三角形的性质,正确的识别图形是解题的关键.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
10.若分式$\frac{x-1}{2x+5}$有意义,则x的取值范围是( )
| A. | x≠1 | B. | x$≠-\frac{5}{2}$ | C. | x$>-\frac{5}{2}$ | D. | x$<-\frac{5}{2}$ |
4.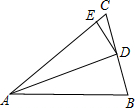 如图,在△ABC中,AB=AC,BD=CD,∠BAD=20°,DE⊥AC于E.则∠EDC的大小是( )
如图,在△ABC中,AB=AC,BD=CD,∠BAD=20°,DE⊥AC于E.则∠EDC的大小是( )
 如图,在△ABC中,AB=AC,BD=CD,∠BAD=20°,DE⊥AC于E.则∠EDC的大小是( )
如图,在△ABC中,AB=AC,BD=CD,∠BAD=20°,DE⊥AC于E.则∠EDC的大小是( )| A. | 20° | B. | 30° | C. | 40° | D. | 50° |

 如图,AB为⊙O的直径,CD⊥AB于点E,交⊙O于点D,OF⊥AC于点F,且OF=1.
如图,AB为⊙O的直径,CD⊥AB于点E,交⊙O于点D,OF⊥AC于点F,且OF=1.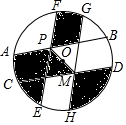 如图,一个半径为2cm的圆盘被分割成十个区域.其中,弦AB、CD关于圆心O对称,EF、GH关于圆心O对称,向盘中投掷一物体,则物体落在阴影部分的概率为$\frac{1}{2}$.
如图,一个半径为2cm的圆盘被分割成十个区域.其中,弦AB、CD关于圆心O对称,EF、GH关于圆心O对称,向盘中投掷一物体,则物体落在阴影部分的概率为$\frac{1}{2}$.