题目内容
5.已知点A(m,m+1)和抛物线y=x2-2mx+m2+m-1上的动点P,其中m是常数,则线段AP的最小值是$\frac{\sqrt{7}}{2}$.分析 根据点P在抛物线y=x2-2mx+m2+m-1上,设p点坐标为P(a,a2-2ma+m2+m-1),表示出AP2,根据二次函数的最值问题得出AP的最小值即可.
解答 解:设P点坐标为P(a,a2-2ma+m2+m-1),
AP2=(m-a)2+[a2-2ma+m2+m-1-(m+1)]2
=(m-a)2+[(m-a)2-2]2
令(m-a)2=t(t≥0)
则有AP2=t+(t-2)2=t2-3t+4=(t-$\frac{3}{2}$)2+$\frac{7}{4}$,
所以,当t=$\frac{3}{2}$ 时,AP2有最小值 $\frac{7}{4}$,
所以AP=$\frac{\sqrt{7}}{2}$,
故答案为$\frac{\sqrt{7}}{2}$.
点评 本题考查了二次函数图象上点的坐标特征,设出点P坐标得到关于t的二次函数是解题的关键.

练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案
相关题目
6.下列计算正确的是( )
| A. | 2a+3b=6ab | B. | 19a2b2-9ab=10ab | C. | -2x2-2x2=0 | D. | 5y-3y=2y |
 用-4、-3、-2、-1、0、1、2、3、4这9个数填在图中.使得横行、竖行、对角线之和为0.
用-4、-3、-2、-1、0、1、2、3、4这9个数填在图中.使得横行、竖行、对角线之和为0.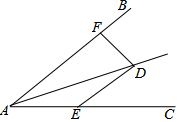 如图:∠DAE=∠ADE=15°,DE∥AB,DF⊥AB,若AE=10,则DF等于5.
如图:∠DAE=∠ADE=15°,DE∥AB,DF⊥AB,若AE=10,则DF等于5.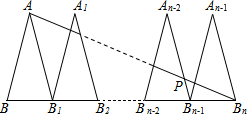 如图,△ABB1,△A1B1B2,…,△An-2Bn-2Bn-1,△An-1Bn-1Bn是n个全等的等腰三角形,其中AB=2,BB1=1,底边BB1,B1B2,…,Bn-2Bn-1,Bn-1Bn在同一条直线上,连接ABn交An-2Bn-1于点P,则PBn-1的值为$\frac{2}{n-1}$.
如图,△ABB1,△A1B1B2,…,△An-2Bn-2Bn-1,△An-1Bn-1Bn是n个全等的等腰三角形,其中AB=2,BB1=1,底边BB1,B1B2,…,Bn-2Bn-1,Bn-1Bn在同一条直线上,连接ABn交An-2Bn-1于点P,则PBn-1的值为$\frac{2}{n-1}$.